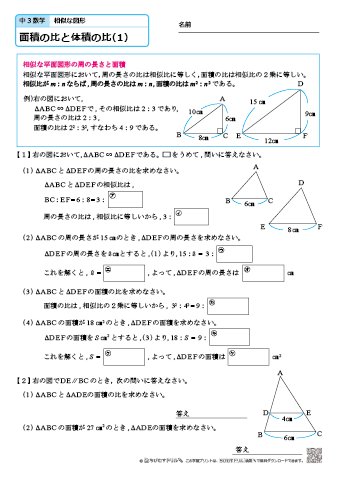
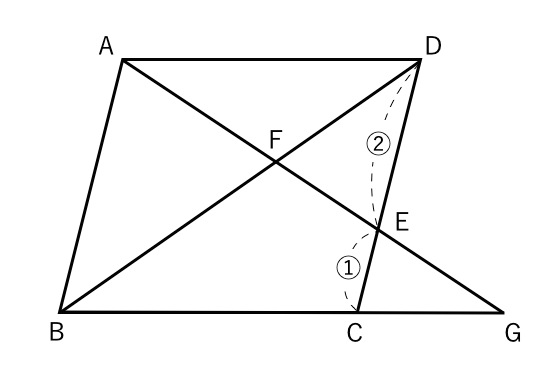
・相似比と面積比・体積比の関係 ・線分比と面積比 について学習しました。学習内容をまとめておきますので,問題を解く前に確認しておきま しょう。 相似比と面積比・体積比の関係 1 相似比と面積比・体積比 相似比と体積比 相似な図形の体積比の問題です。 基本を確認して、いろいろな応用問題を解けるようにしてください。 基本事項 相似比が a b である図形の面積の比は, a3 b3 である。 *簡単な証明もできるようにしましょう。相似比の練習問題(平行四辺形例題) 底辺の比=面積比=1:2 より fbc =5 ×2 =10 cm2 相似比1:2 →面積比1:4 より fcd =5 ×4 =cm2 問7.平行四辺形abcd の辺ab,ad の中点をそれぞれe,f とし対角線bd と線分cf の交点
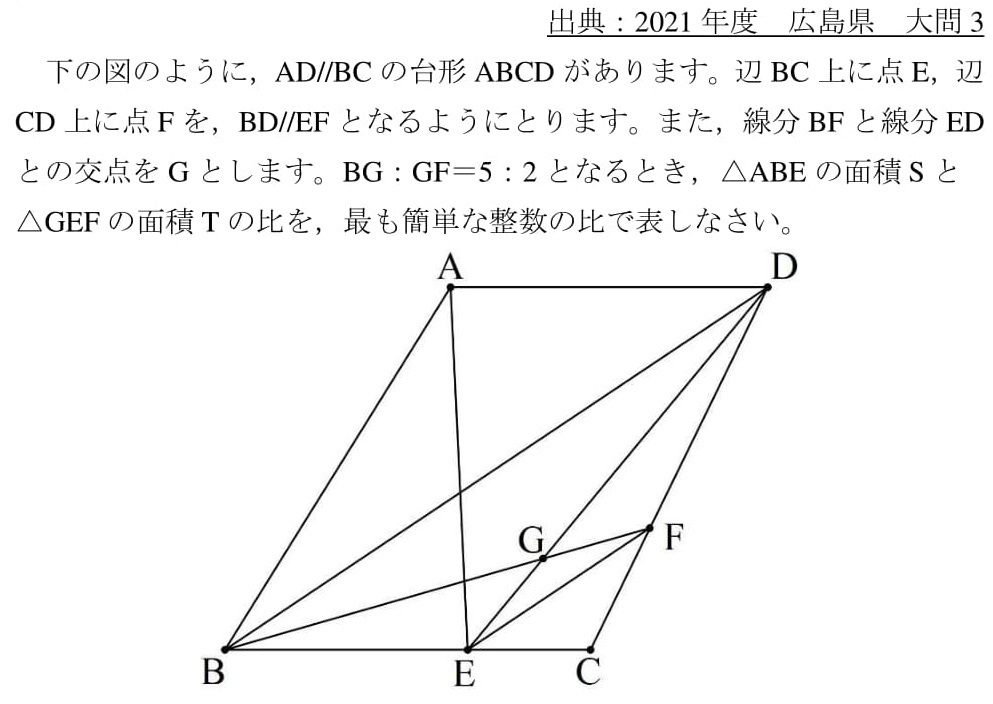
中2で解ける線分 面積比問題 21広島県大問3 高校入試 数学 良問 難問
線分の比と面積比 問題
線分の比と面積比 問題-STEP 1 : A D O ∽ C B O A D C B = 12 c m c m = 3 5 (相似比) POINT:対応する線分の長さの比は、すべて等しい STEP 2 : A E O ∽ A B C ( B E O ∽ B A D でもOK) ③ ③ ⑤ A O A C = ③ ③ ⑤ = 3 8 (相似比) 3 8 = a これを解いて、 a = 15 2 STEP 3 : D F O ∽ D C B 同じようにウ 平行線と線分の比についての性質を見いだし,それらを確かめること。 エ 基本的な立体の相似の意味と,相似な図形の相似比と面積比及び体積比の関係について理解す ること。 オ 相似な図形の性質を具体的な場面で活用すること。



数学i Aチェック リピート 第4章 2図形への応用 8 相似形の面積比 Pukiwiki
線分比→平行 問題(3 学期) 次の文は,三角形と線分の比についての定理である。( ) をうめよ。 abc で,辺ab,ac 上の点を,それぞれp,q とする。 (1) pq // bc ならば, ap:ab=aq:( ア )=pq:( イ ) (2) ap:pb=aq:qc ならば,pq // ( ウ ) 解答欄 ア イ相似・線分比と面積比 レベルaの25題 問1 右の図でabとcdが平行なとき、ア〜エの長さを求めなさい。 問2 右の図でabとcdが平行なとき、ア、イ、ウの長さを求めなさい。 問3 右の図形はある土地の1:00の縮図です。この土地の実際の面積が何m2 この「入試問題にチャレンジ」コーナーでは、入試の基礎となる問題を選び、受験生がまちがえやすいポイントを丁寧に解説しています。 算数図形編面積比・線分比・相似 面積比を辺の長さで表そう 中学受験 高校受験パスナビ
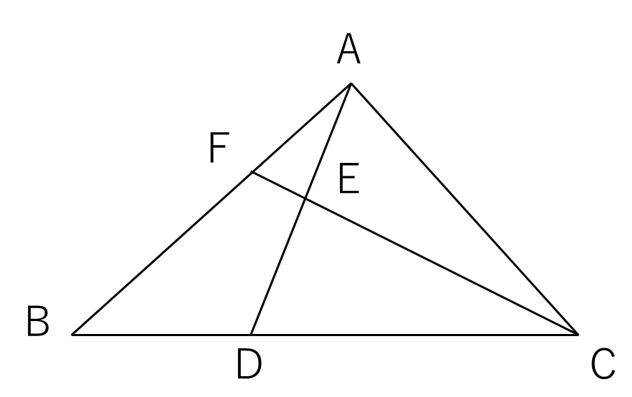
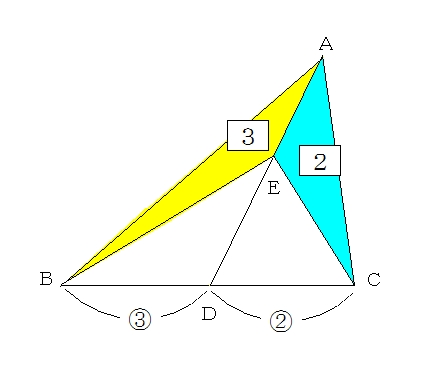
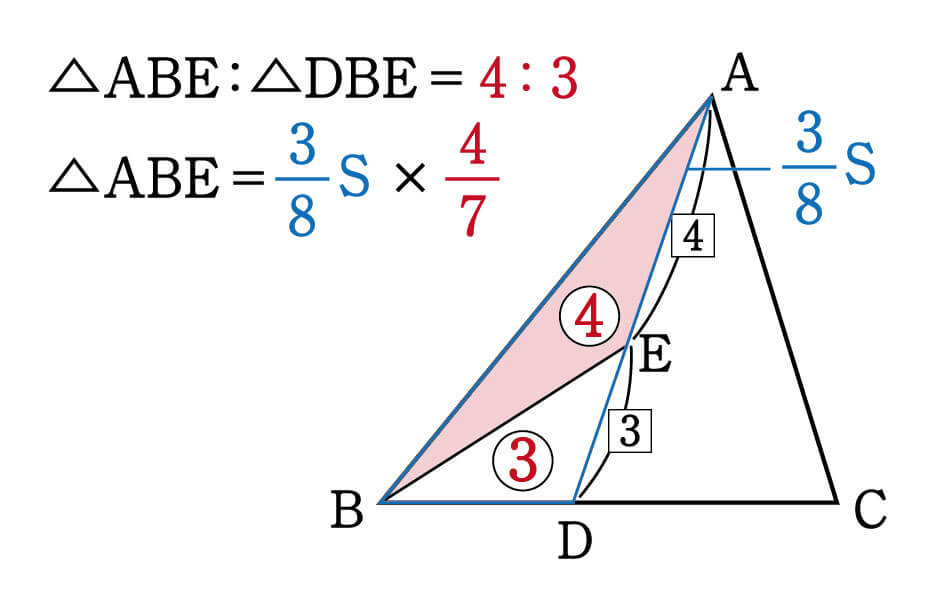
線分比・面積比の応用問題です。三角形の山型相似がテーマです。 応用問題105 02 中2以上。線分比・面積比の応用問題です。三角形の山型相似がテーマです。比の方程式がでてきます。 応用問題106 01 小6以上。線分比・面積比の応用問題です。この問題教えてください💦線分比と面積比のところです💦 B ん / 右の図のように, AABCの辺BC上に点D, 人A 線分AD上に点をそれぞれ AE ED=2 1 BD DC=ニ3 4 となるようにとる。このとき, AABE とAEDCの面積比を求めなさい。 審 み4D・ のPB ぜひ挑戦してください!受験生がまちがえやすい問題やポイントをもっと学習したい方は、本書をご購入ください。 算数図形編 でる度⇒ ★★★《面積比・線分比・相似》全体の面積を比で
数学35章図形と相似「平行線と線分の比」<基本問題①・解答> 1 説明※平行線は,三角定規を利用してかく。 ①図のように線分AC上で点Aから 7番目の点と点Bを結ぶ。 ②点Aから5番目の点を通り,①で ひいた線分と平行な線分をひく。平行線と線分の比 まとめ 以上、7パターンの問題について解説してきました。 おそらくこれらのパターンをしっかりと理解できていれば ほとんどの問題には対応できるのではないかと思います。 比の取り方は、練習で身につけていくのが一番です。面積比+底辺比 問題(2 学期期末) 右の図で,de // bc,ad:db=1:2 である。be と cd の交点をf とするとき,次の各問いに答えよ。 (1) edf と bcf の面積比を求めよ。 (2) edf の面積が8cm



3




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
基本的な立体の相似の意味と、相似な図形の相似比と面積比、および体積比の関係について理解し、問題でくり返し練習します。 面積の比と体積の比(1) ⇒ 答え 面積の比と体積の比(2) ⇒ 答え 面積の比と体積の比(3) ⇒ 答え 面積の比と体積の 面積比と線分比とチェバの定理 まずは、面積比ってなに? ってあなたは、こちらで理解しておいてほしいんじゃ おーい、ニャンコくん、面積比と線分比の関係についての解説記事をお願い! 数学にゃんこ はーい、先生! 面積比と線分比については2つの線分の交点の位置ベクトルや 内分比を求める裏技(教師用) 札幌東高校 佐藤 清 はじめに ベクトルの単元のいわゆるst問題を扱ったときに,ふとしたはずみで下の問題のような2つの線分の交点の位置ベクトル,あるいは各線分の内分比を求める簡易的方法(裏技)に気がついたので今回



線分の比と面積比についての質問です この問題の 3 5になって Yahoo 知恵袋



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ
相似な図形と線分比と平行の関係、その計算方法と図形をとらえる視点について応用問題を含めて学習します。 三角形と線分比 平行線と線分比 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と面積比の問題の解法 線分比と面積比の性質を使った問題です。 基本となるのは線分比です。 与えられた情報から新しい情報を導くことが基本となることは変わりません。 記事を 中2で解ける線分・面積比問題(21広島県大問3) スポンサーリンク 中2でも解けるので,今の時期,何か難しめの問題解きたいときにおすすめです。 広島県の全部の問題はコチラ( 広島県ホームページ ) 大問1以外は記事にしました。 ・大問




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




中2で解ける線分 面積比問題 21広島県大問3 高校入試 数学 良問 難問
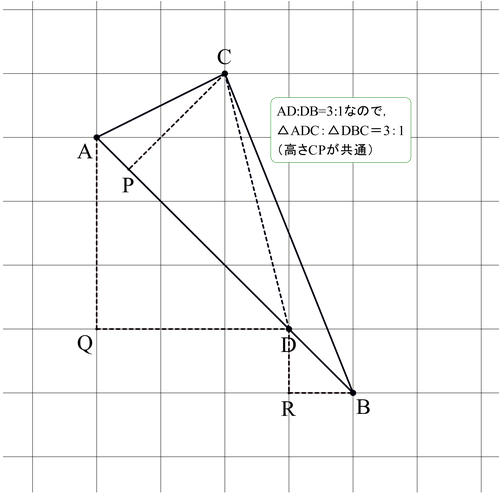
中2で解ける線分・面積比問題(21広島県大問3) 無理ですね(21広島県大問2)(写経問題と中線定理) 関数平行移動と無理やりな教育的・新共通テスト意識問題とGRAPESの使い方(21年宮城県)面積比の問題 図形問題の難問で良く使われる「面積比」の問題について 解説しておこう。 一部の辺に比が与えられて、「面積比を求めよ」と言う問題 だ。「 2倍である事を示せ」とか「面積が等しい事を示せ」と 言うのも、同じ問題だ。 さて、今回は、中学三年生の数学「相似」という単元の中の「三角形の線分の比と面積の比」の話。例題 上の図で、ADDB=23、BEEC=41である。 BDEの面積は ABCの面積の何倍であるか答えなさい。この問題には何通りかの解き方がありますが、どれも、,セギ英数教室 角木優子 の塾




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su



熊先生の学習法
(1)の解説はこちら←年度 千葉県公立高校入試問題・前期数学 第四問1 (円周角の定理) 解答 前半 (1)を使って fbeの面積を求める また(1)より ead ∽ efb。故に相似な三角形の辺の比は等しくadde=fbbe=13 be=6よりfb=2 線分比を求められれば面積比を計算できます。 面積比が分かれば体積比を計算できます。 というように線分比が分かるというのは図形問題において後半戦を乗り切るのに重要な事なのです。 よって連比をマスターする事による恩恵は計り知れないと言える4 章の確認・章末問題 10 3 115中学の数学幾何Ⅱ_H_p0003indd 35中学の数学幾何Ⅱ_H_p0003indd 3 AM621 AM Title



ややこしや 線分の比 と 面積の比 名寄 算数数学教室より



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード・印刷 基本的な立体の相似の意味と、相似な図形の相似比と面積比、および体積比の関係について理解し、問題で練習します。相似分野の応用問題①ラスボスっぽいの,多分それ連比です。 面積の比 (何倍)を求める問題も含めてかんたんな方法を解説します 教遊者 If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations To



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




高校数学a 三角形の面積と線分の比 練習編 映像授業のtry It トライイット




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



線分比と面積比 クソオリジナル問題 高校入試 数学 良問 難問




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生



辺の比と面積比




平面図形をマスター 三角形の面積比 応用編その2




補助線の引き方 日々の学習 兄中学受験



Studydoctor線分の比と面積比 中学3年数学 Studydoctor



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor




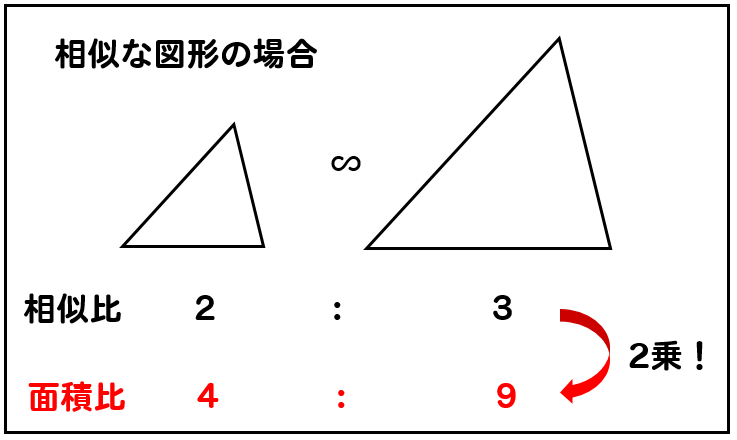
3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



Studydoctor平行線と台形 中3数学 Studydoctor




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




39 面積比から線分比を求める Youtube



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




無料 中3数学 標準問題 解答プリント 328 図形の相似3 線分の比




高校数学a 三角形の面積と線分の比 例題編 映像授業のtry It トライイット




北辰塾 情報局 直撃 中学入試問題 第311回 東邦大東邦 平面図形 線分比と面積比
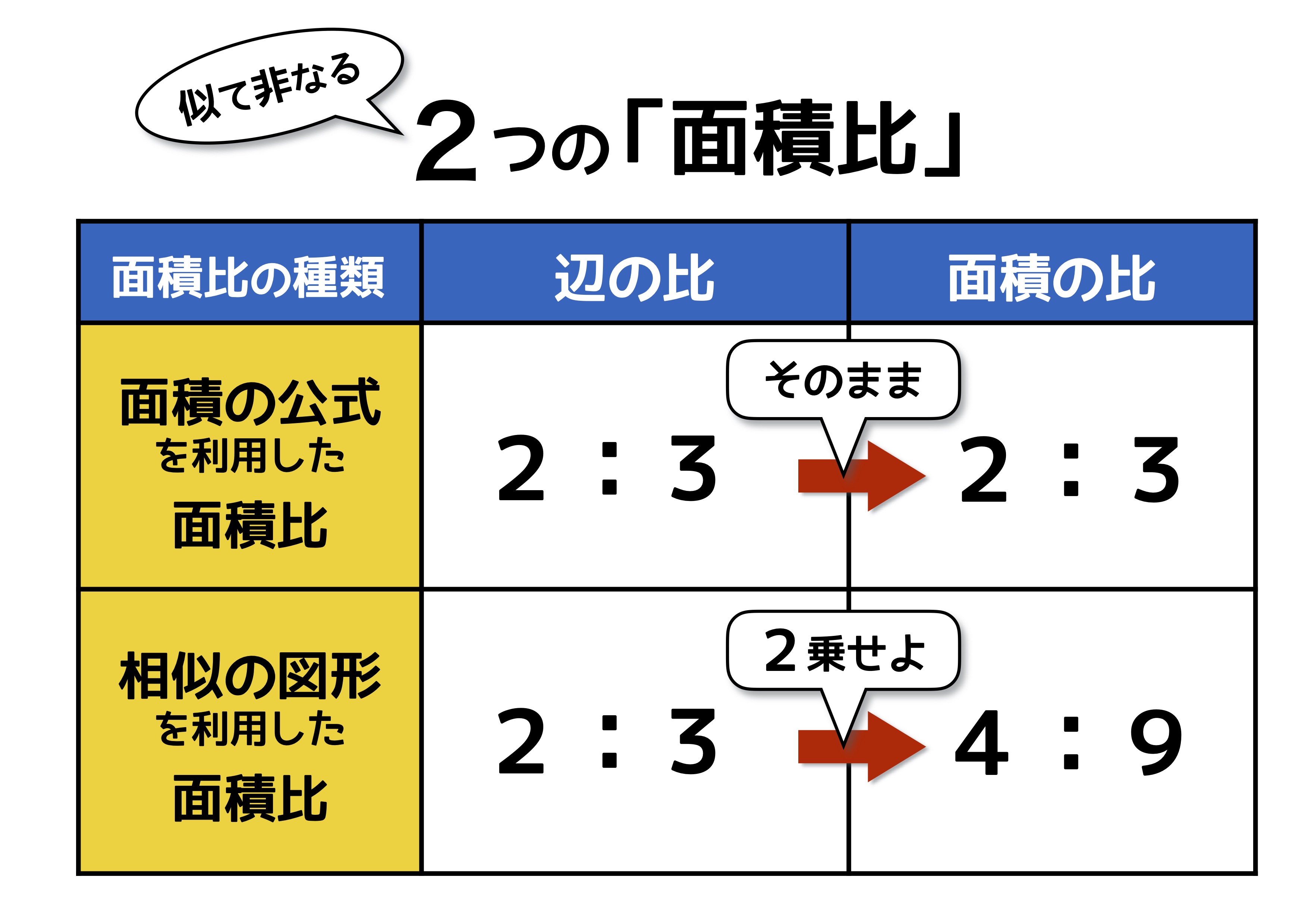



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
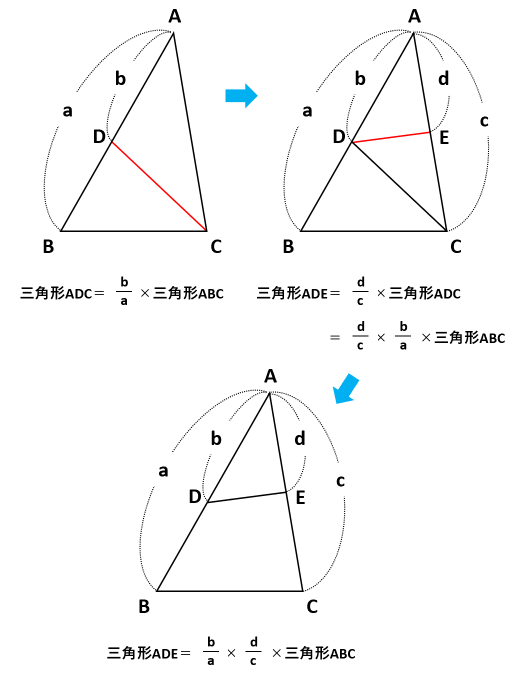



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor



数学i Aチェック リピート 第4章 2図形への応用 8 相似形の面積比 Pukiwiki




Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ
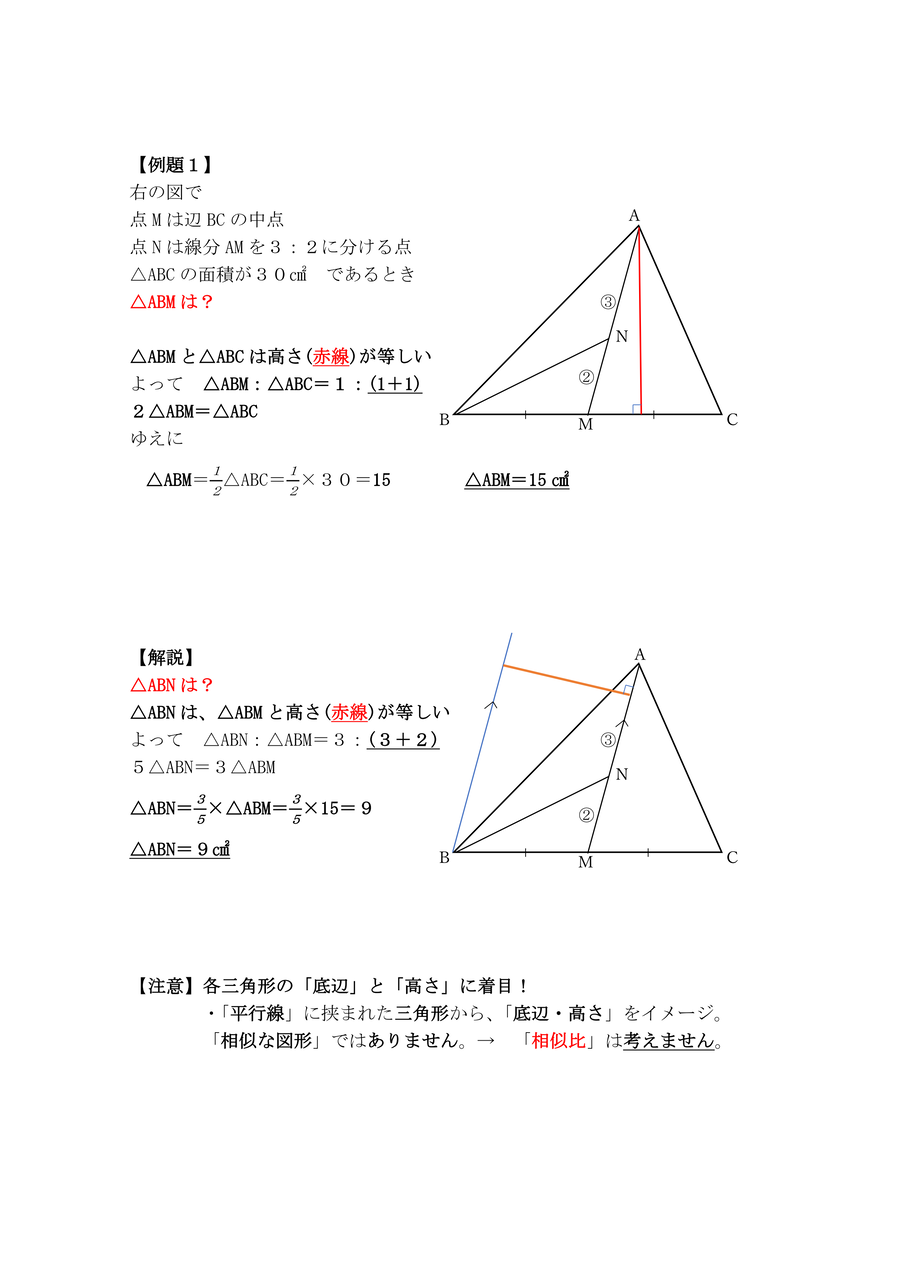



中学校数学 証明のコツ 面積比 体積比



今月の問題 平行四辺形
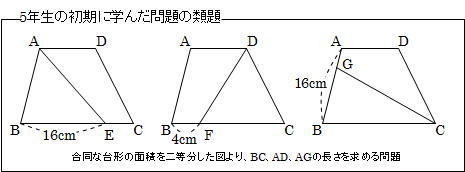



小5の学習ポイント4 辺の比と面積比 前田昌宏の中学受験が楽しくなる算数塾
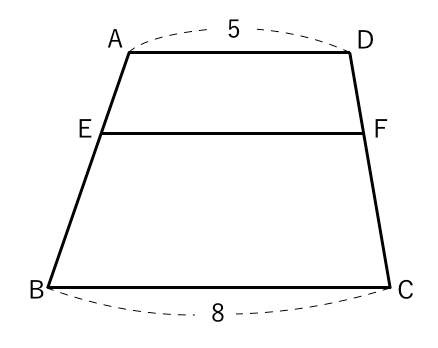



相似な図形 計算 台形 練習問題 苦手な数学を簡単に
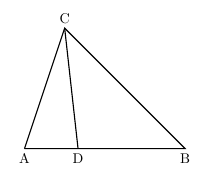



線分比と面積比の問題の解法 夢を叶える塾
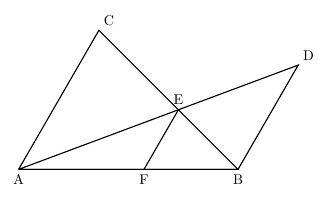



線分比と面積比の問題の解法 夢を叶える塾
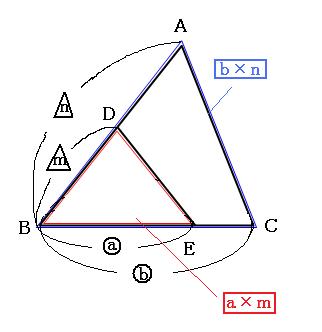



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める
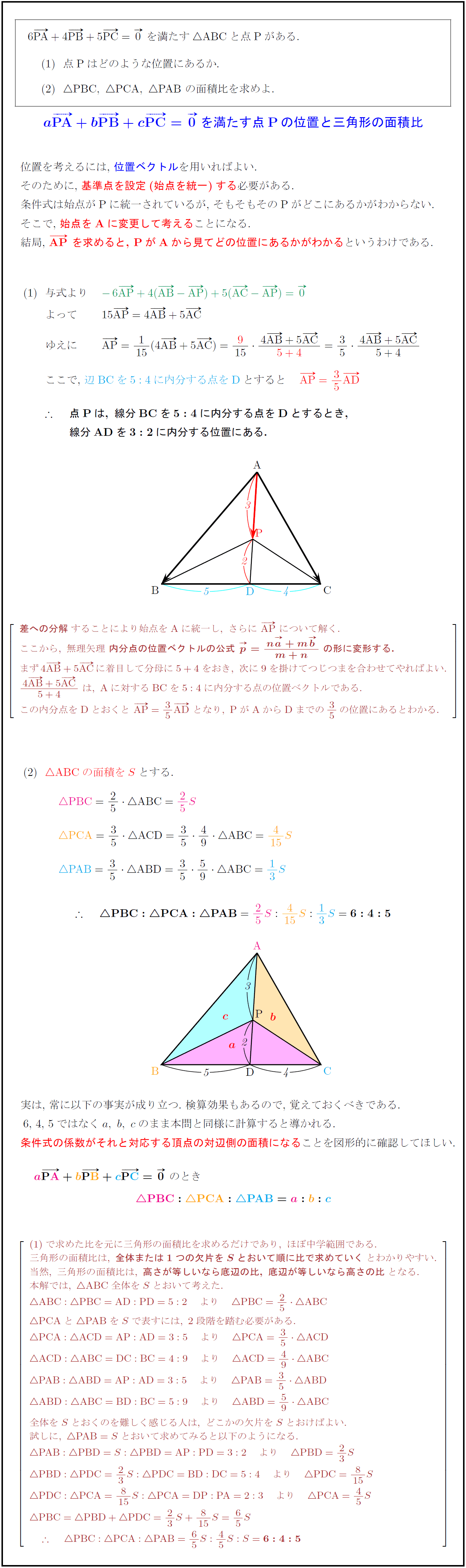



高校数学b Apa Bpb Cpc 0を満たす点pの位置と三角形の面積比 受験の月




平面図形をマスター 三角形の面積比 応用編その3
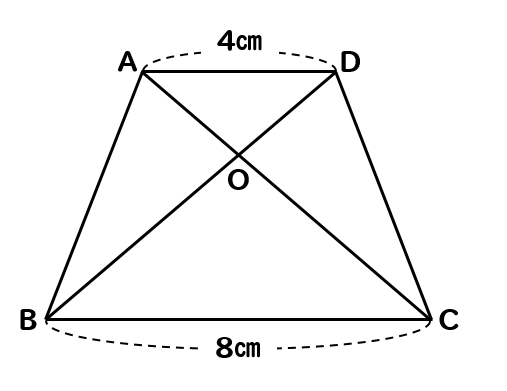



相似 台形と面積比の問題を徹底解説 数スタ




応用 ベクトルの等式と三角形の面積比 なかけんの数学ノート
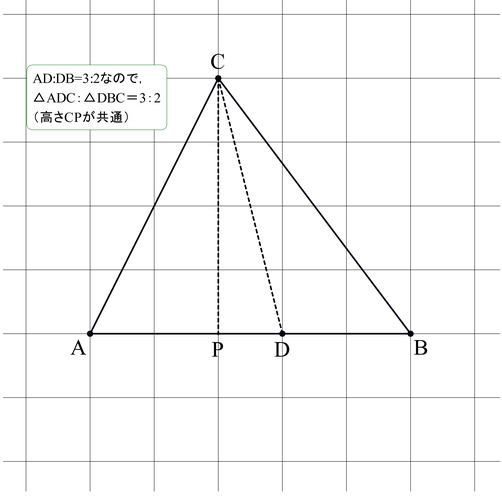



線分比と面積比 クソオリジナル問題 高校入試 数学 良問 難問




面積比 2つの三角形で高さが同じときの面積比 身勝手な主張



なぜ比を2乗したら面積比になるのですか 例えば比が1 2の相似な Yahoo 知恵袋




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学
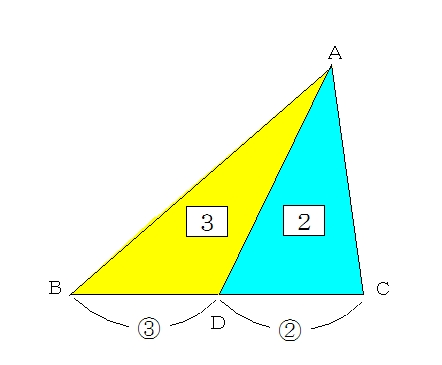



辺の比と面積比




辺の比と面積比問題 考え方1 Youtube




線分の比と面積比の問題です Fg Gcを求めよ Clear



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
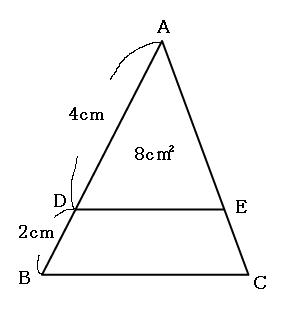



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




平面図形の苦手を解消 三角形の面積比 基本編
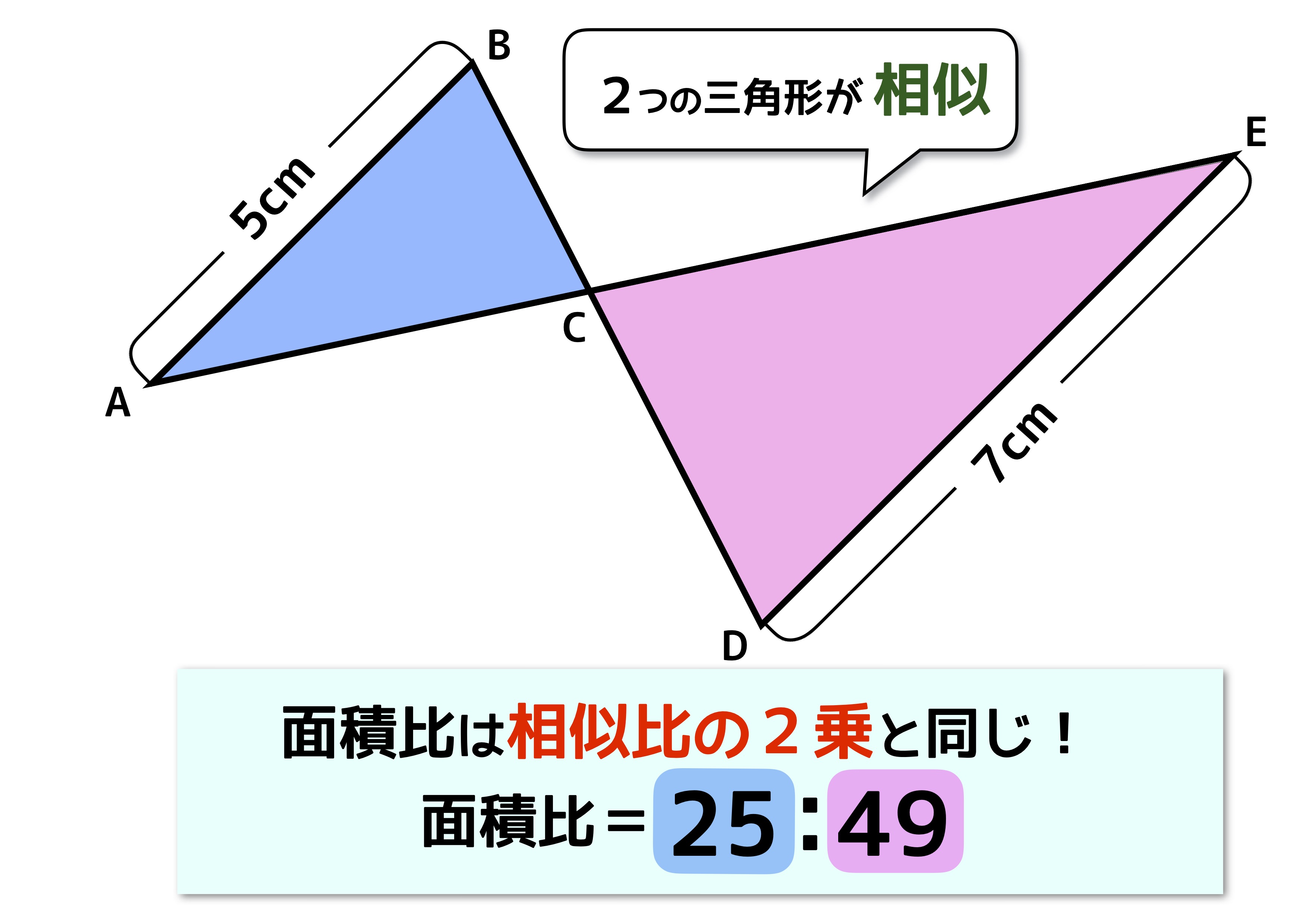



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
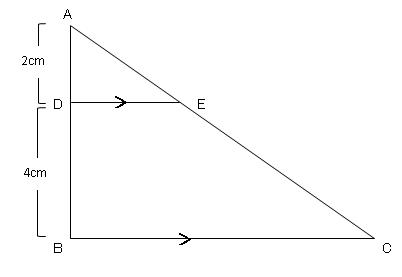



相似と面積比 1 ネット塾
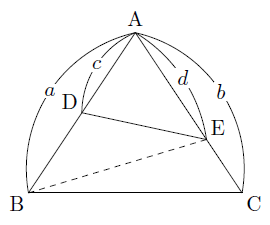



1角共有の三角形の面積比 まなびの学園
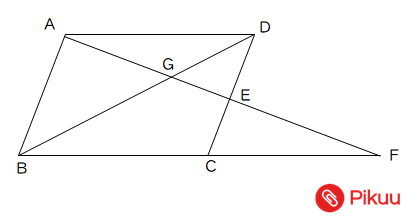



高校入試対策数学 面積比に関する対策問題 Pikuu




中3 20 1 線分比と面積比 1 Youtube




高校入試対策数学 面積比に関する対策問題 Pikuu




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問



中3数学12 図形の相似3 線分の比 発展問題プリント 問題 328
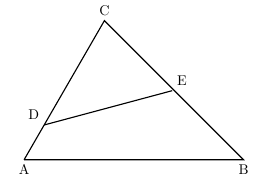



線分比と面積比の問題の解法 夢を叶える塾




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
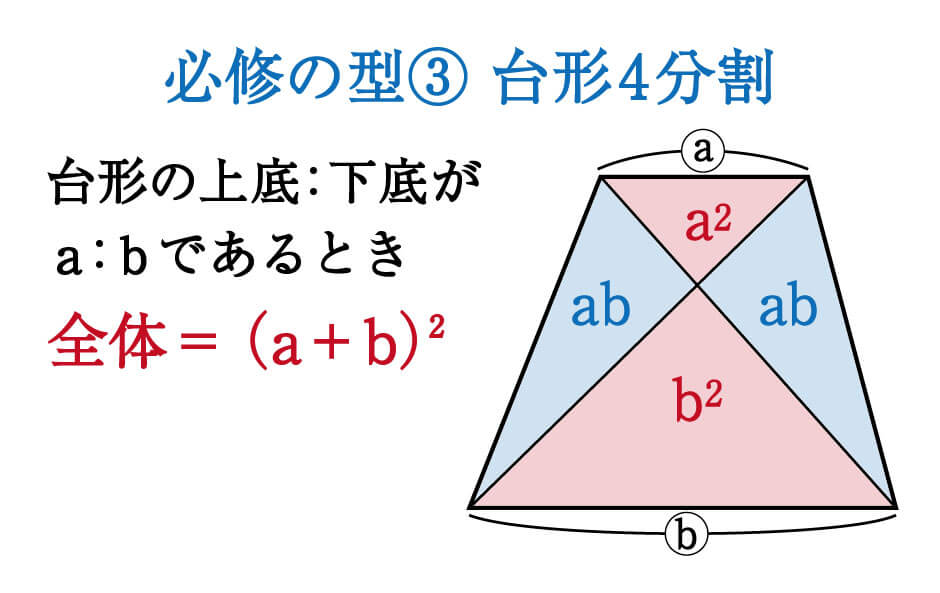



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




相似 平行四辺形と面積比の問題を徹底解説 数スタ



芝11 5 平面図形 線分比や相似を利用して面積比を求める問題 気まぐれ解説カフェ 仮



相似 平行線と線分の比 の分野です 面積比の問題なのですが Yahoo 知恵袋




三角形の面積比 数学の偏差値を上げて合格を目指す
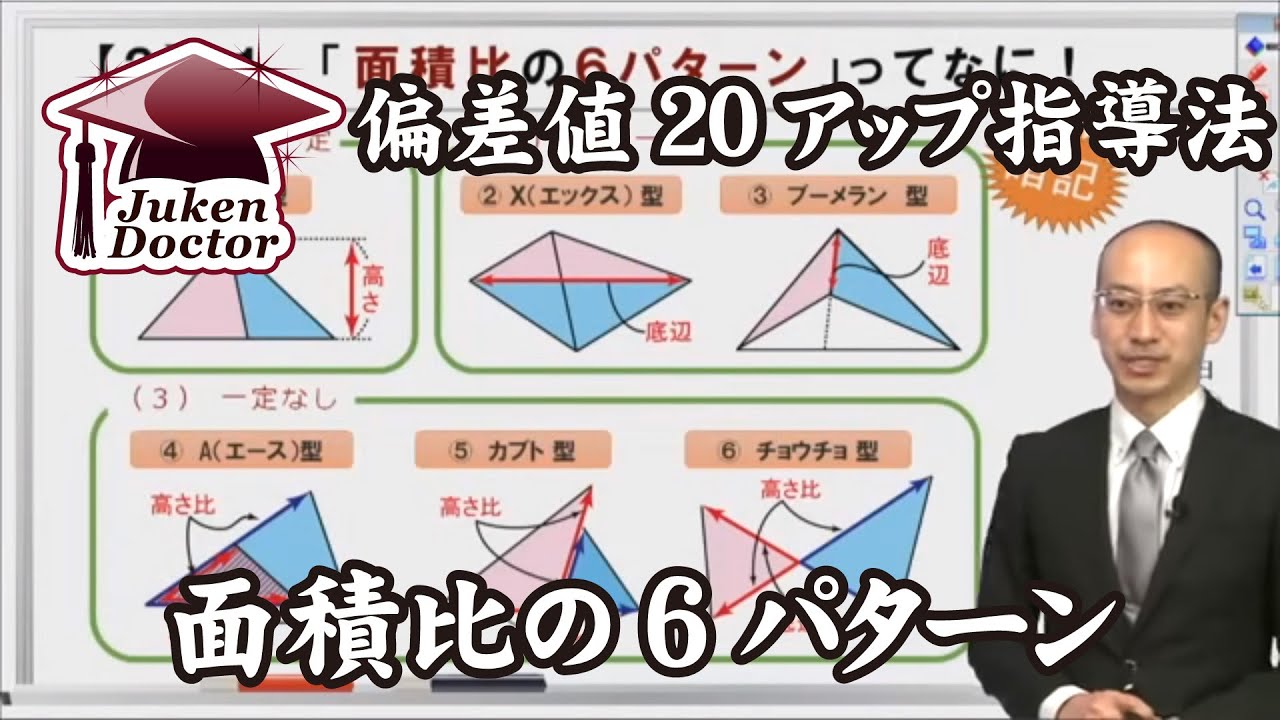



8 面積比の6パターン って 中学受験ドクター Youtube




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




相似の面積比を求める問題 上級編 Youtube




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube
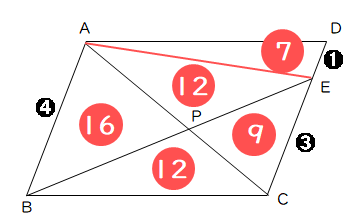



高校入試対策数学 面積比に関する対策問題 Pikuu
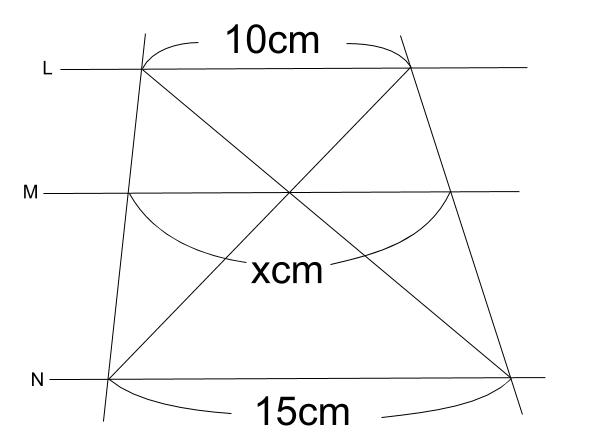



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



平行線と線分の比 辺の長さを求める応用問題4選 教遊者




数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生




Dfeの面積と平行四辺形の面積比の問題です Clear



公立高校入試2019 図形 中学から数学だいすき
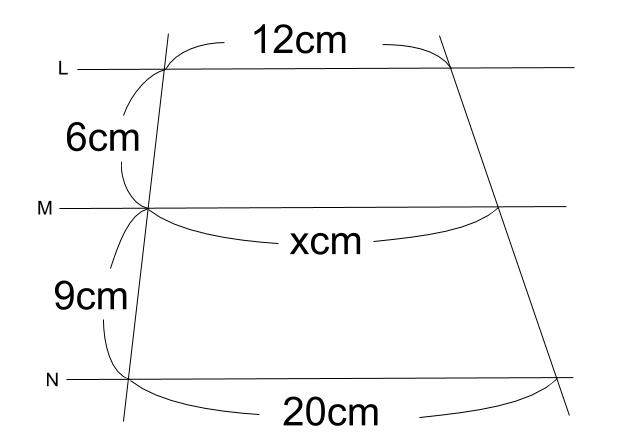



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



相似 平行四辺形と面積比の問題を徹底解説 数スタ




この問題教えてください 線分比と面積比のところです Clear
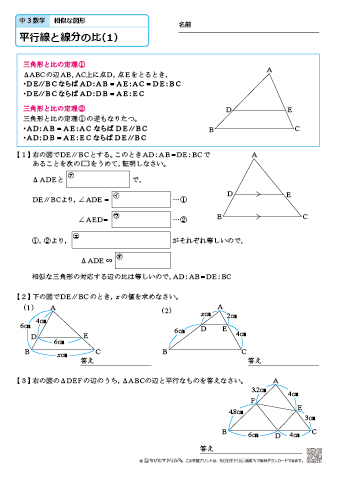



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



高校入試数学 面積比のポイントと練習問題




平面図形をマスター 三角形の面積比 応用編その2




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座




相似 平行四辺形と面積比の問題を徹底解説 数スタ
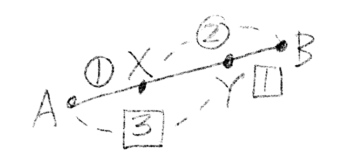



中学受験 底辺比と面積比のまとめ 小学生 そうちゃ式 受験算数 2号館 図形 速さ



1




数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



3
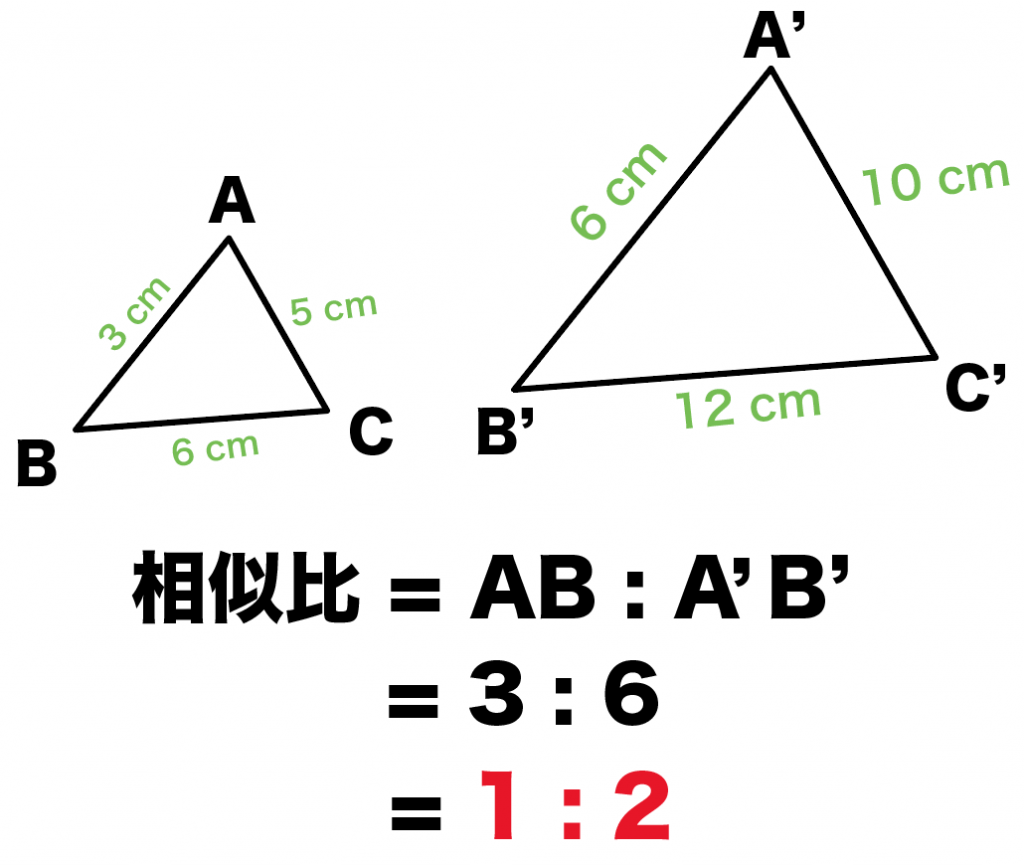



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



1
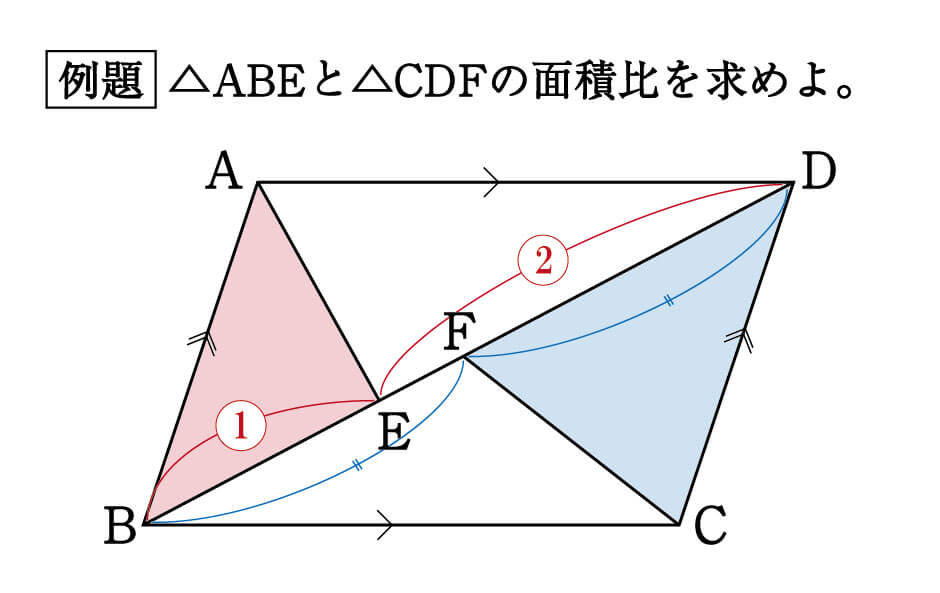



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




線分比 面積比 体積比 数学カフェjr




平面図形をマスター 三角形の面積比 応用編その3
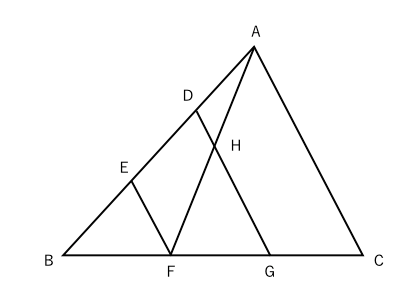



面積が何倍かを求める問題 応用編 苦手な数学を簡単に




算数図形編 面積比 線分比 相似 面積比を辺の長さで表そう 中学受験 高校受験パスナビ



0 件のコメント:
コメントを投稿