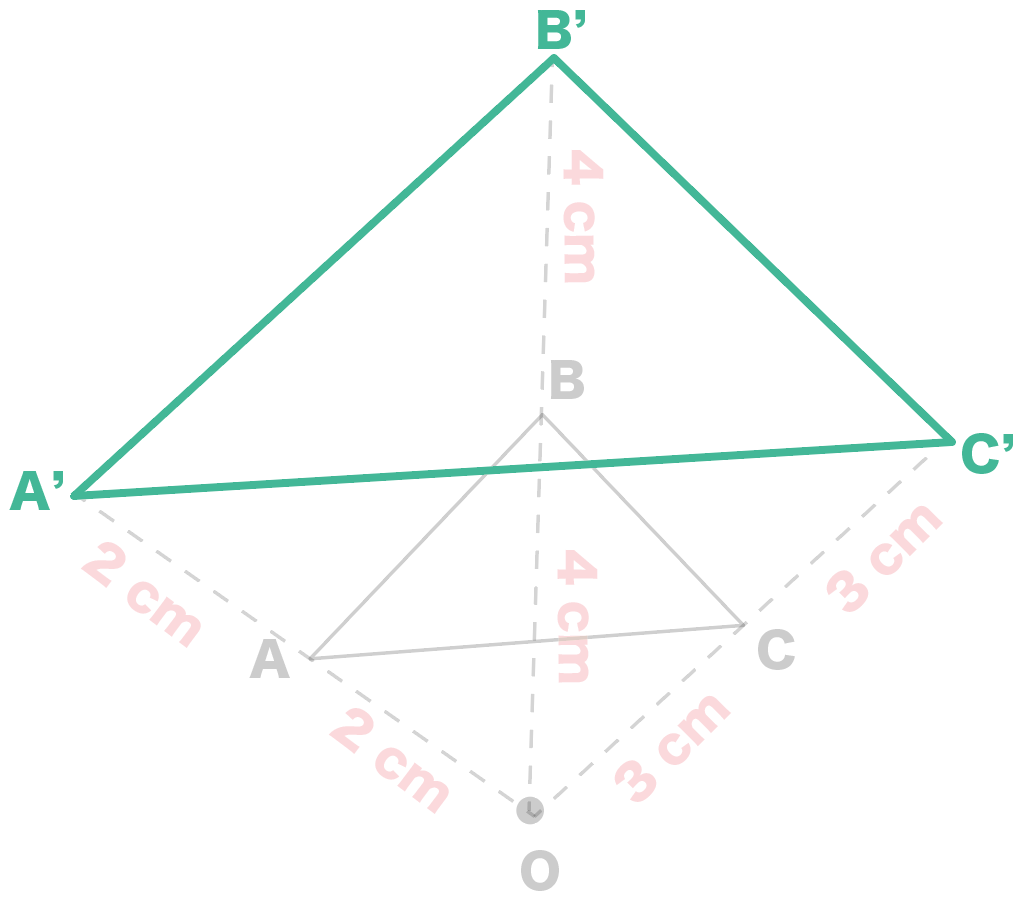
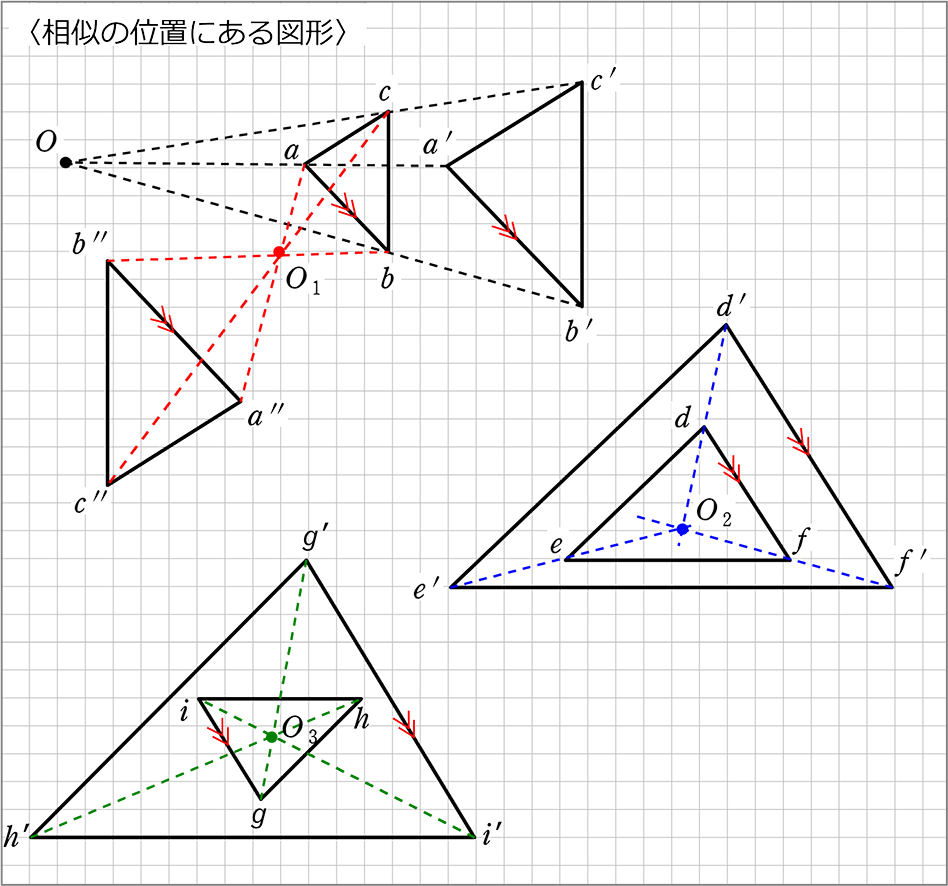
A・相似な三角形を自力で3通り作図できる。 B・相似な三角形をヒントを手がかりに3通り作図することが できる。 知識・理解 A・なぜ相似の関係となるかを定義を使って説明した記述があ る。 B・相似であるかどうかを判定できる。 6 単元指導計画相似な図形は形が同じだから対応する角はそれぞれ等しいよね! 対応する辺の長さはすべて 2倍 になっている。 またこの 2 つの図形は 1点O を通る直線を利用して作図されて いる 2倍 の拡大図だね。6「相似の中心として相似の位置にある」の意味 ≪一斉≫ 7 相似の中心からみて、もとの図と反対方向に 直線をひき、相似な図形を作図する ≪ペア≫ 8 相似の中心を適当にとって、相似な三角形を 作図する ≪個≫ ⇒ ≪3~4人グループ≫
中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
相似の位置 作図
相似の位置 作図- この記事では、高校入試に出題された作図問題の解き方を解説していきます。 数学の入試問題では 作図は必ずと言ってもいいくらい出題される 必須の問題ですね! しっかりと対策しておけば 得点源にすることができる単元でもあるので この記事を相似の位置 作図 相似の位置 作図 要使用 查找相似位置 工具,您需要提供参考位置、候选搜索位置和表示匹配条件的字段。 针对分析选择的图层应包含参考位置或基准 位置。



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 047 Pdf
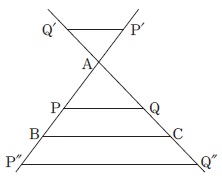
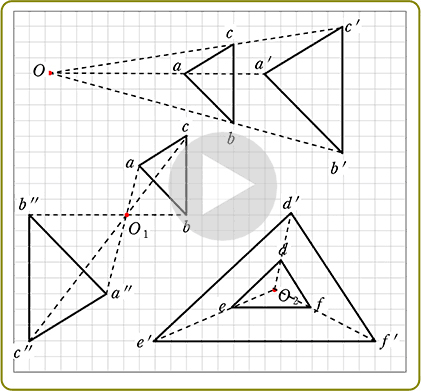
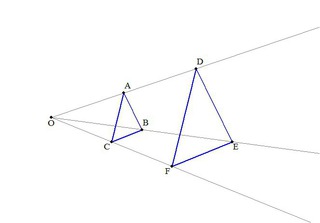
前ちゃんの中学校数学の部屋:プレゼン教材ダウンロード一覧 プレゼン教材直接ダウンロード一覧 プレゼン教材を ワークシートと一緒に学年・学期・単元ごとに一覧表にしています。 直接リンクですので クリックするだけでダウンロードできます授業実践記録(数学) 1.はじめに 授業の形態や課題を工夫する事で楽しみながら学習できれば,意欲,定着度,思考力, 表現力などを高めていけるのではないかと考えた。 そこで,図形と相似の導入で以下の点に留意しながら授業実践を行った。 尚相似の中心o が三角形の内部にあるときも同様である。 下の図は,点o を中心として,4abc を3 倍に拡大した 4def をかいたもので,どちらの場合でも4abc と4def は相似の位置にある。 a d e f b c o a d e f b c o oa od,ob oe,oc of がどれも1 3 になっている ことを確かめよう。
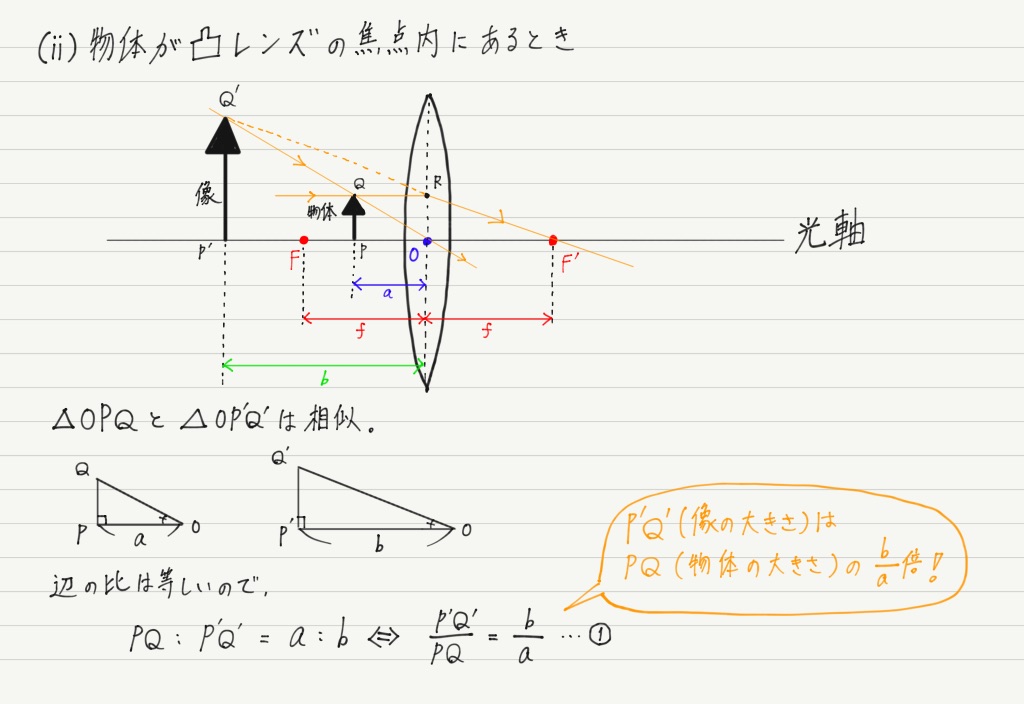
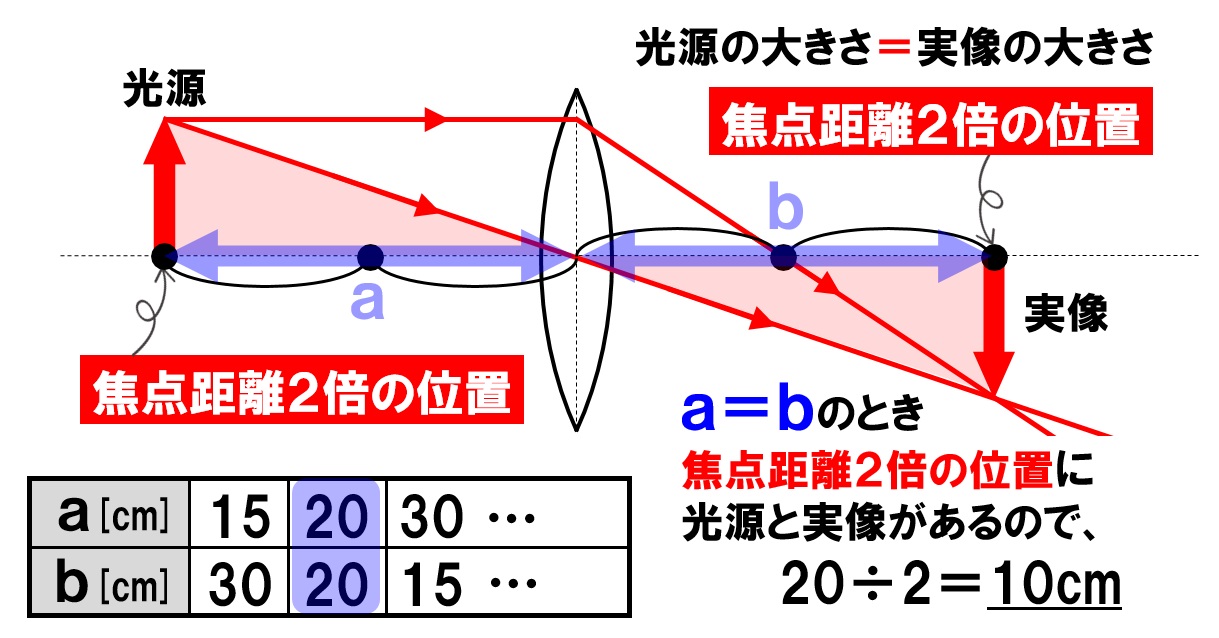
光軸に平行な光とレンズの中心を通る光を作図すると、P'Q'の位置に倒立の実像ができますね。 像を位置を物体の位置と焦点距離を使って表すために、三角形の相似関係を使います。 赤の三角形 と 青の三角形 は "3つの角が等しい" ので相似です。辺の・相似の意味と記号∽を使った 相似の表し方を理解する。 (1) ・2つの三角形が相似であるか どうかを判断し,記号∽を用 いて表すことができる。 ワークシート 自己評価表 三 ・相似の位置や相似の中心2乗の作図とグラフ その他の関数 3次関数のグラフ 3次関数の接線の本数 y = x 1/x のグラフ 三角関数の定義 1/x の作図とグラフ 平方根の作図とグラフ 座標平面における図形 放物線に接する円 類題 放物線と円の共有点
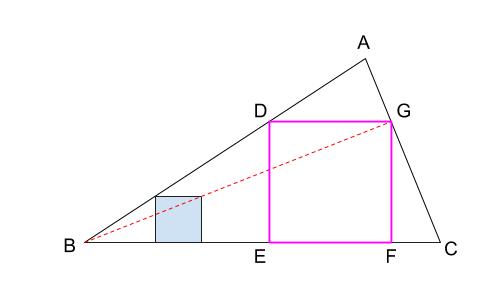
2 相似な図形の性質や相似比について理解させる。 イ-① エ-① 3 相似比を利用して,対応する辺の長さを求めることができるようにする。 ウ-② 4 拡大図のかき方を通して,三角形の相似条件を理解させる。 イ-② ウ-③ エ-② 5ずばり、作図方針は「相似の利用」です。ピラミッド型の三角形を利用します。 下図のような図が目標です。 どうやって作図するのかは、後の話です。今は、\(p\) が、\(ab\) を \(12\ の位置です。 ※平行線の作図は、ひし形の作図です。※「相似の位置」が出ている教科書と,出ていない教科書がある。 右の図の2 つの長方形は相似の位置にある。相似の中心o の 位置を作図によってすべて求めよ。




中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1
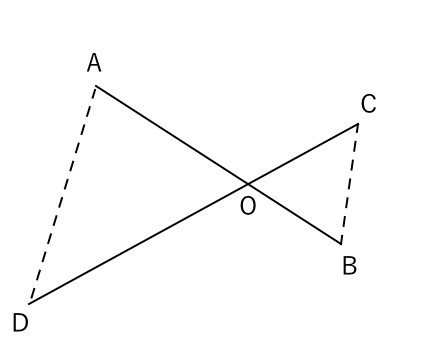
方眼のない拡大図や縮図の作図を通して、相似の位置関係を意識することから相似の意味の理解を深め させる。 ・三角形の相似条件、三角形と比、平行線と比、中点連結定理、相似比と面積比、体積比の学習へと発展 させていく。中学数学 相似な図形の内容 z 相似な図形の性質 z 相似の位置 z 相似比 z比の値 z 三角形の相似条件 z 三角形の相似条件を使った証明 z 相似の利用(測量) z 三角形と比 z 三角形と比の定理の逆 z 中点連結定理 z 平行線と比 z 三角形の角の二等分線と比 相似の中心、相似の位置、とはいったいなんですか。 ベストアンサー:2つの相似な図形において、 ① 対応する辺がそれぞれ平行 ② 対応する点を結ぶ直線がすべて同じ点を通る この2つを満たすとき、 2つの相似な図形は 「相似の位置」 1 12/8/16 11



Www Kurims Kyoto U Ac Jp Kyodo Kokyuroku Contents Pdf 19 07 Pdf



学習指導要領ナビ Jp 中学校 数学 第3学年の内容 b図形 図形の相似
相似な図形の性質 相似な図形の基本事項に関するプリントです。 相似な図形の基本や相似比、相似の記号(∽)などをしっかり確認しておきましょう。 また、相似な図形の長さを比で計算出来るようにすることも大切です。 *プリントは追加する予定そして,図形に関わる定理,作図を用いて,「サッ カーのパス」に関する問題を解決する教材の開発を行った。本論文では,その教材の内 容について報告する。 <キーワード>サッカー,直角三角形,三平方の定理,三角形の相似,作図 1 はじめに相似な図形とは?中学3年数学 相似比と辺の比中学3年数学 相似の位置と中心中3数学 相似な図形や中心の作図中3数学 三角形の相似条件中3数学 相似な三角形の辺の比中3数学 21相似の証明 相似の証明の基本その1中3数学



2




授業実践記録 数学
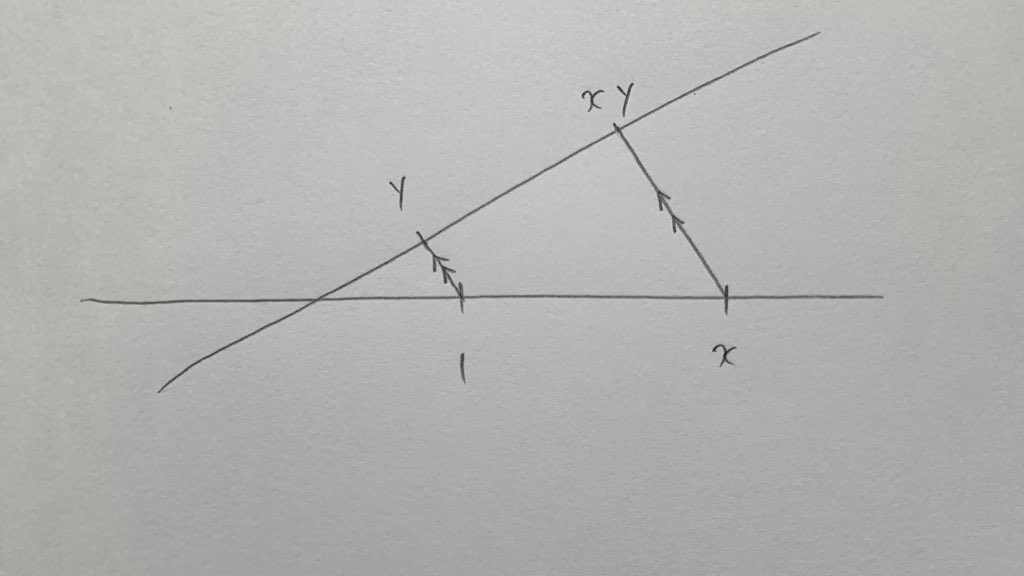
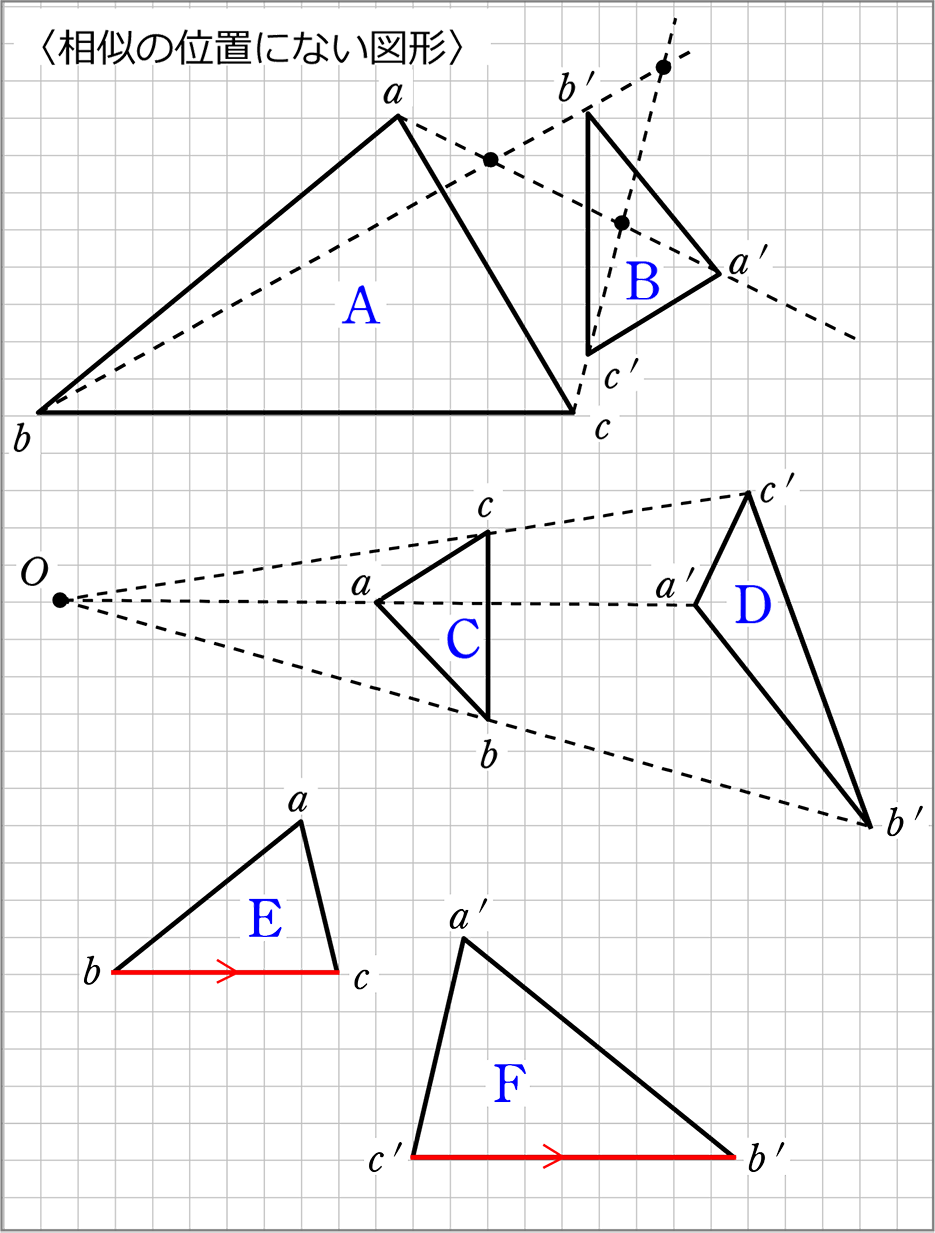
この相似条件は1番簡単で、でてきやすい相似条件なんだ。 たとえば、次の abcと defを想像してみて。 ∠abc = ∠def = 48° ∠acb=∠dfe = 50° この場合、2つの三角形は、「2つの角がそれぞれ等しい」っていう相似条件に当てはまるから、相似であるといえるんだ。半径の異なる円は,必ず相似の位置にあります. 相似の中心は,2円の中心を 半径の比に内分した点,外分した点と2点あります. もし2円に共通外接線,共通内接線が が引ければ,交点が相似の位置の位置の中心です.相似でかつ相似な位置に描かれた 図形の和に等しい と主張する。 相似でかつ相似な位置に図形を描くのは 命題6ー18(作図線分上に相似な直線図形) による。 ここでの図は、 相似でかつ相似な位置にある 長方形であるが、 証明そのものは



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋




動画で学習 3 相似の位置 数学
課題の定着 課題5 相似の中心を、図 次の図で、相似の中心oを自分で決めて、 abcを 形の外部にとってÑ に縮小した a'b'c'を描きなさい。 も外部にとっても 作図できることに 複数の生徒に描かせ、それらを分類する。 気づかせたい。となっている.この作図法は文献2を参考にした. b a abo o 2 o 1 図8 アポロニウスの円を用いる(解2) 4.定規だけで作図する方法 以上は不動点を求める代表的な作図法であるが,冒頭で述べた合同変換の作図法が相似変換にも適用でき相似の基本性質 まとめ それでは、最後に簡単なまとめをしておきましょう。 相似な図形とは 拡大、縮小の関係にある図形のことでしたね。 記号を使って、このように表すことができます。 相似な図形の性質とは 対応する辺の長さの比は、すべて



Http Www Rs Tottori U Ac Jp Mathedu Mt Xue Sheng Zuo Pin Files J3 Pdf




中学数学 作図 下の写真に写ってる2番の問題なんですが 答えを見たところ Okwave
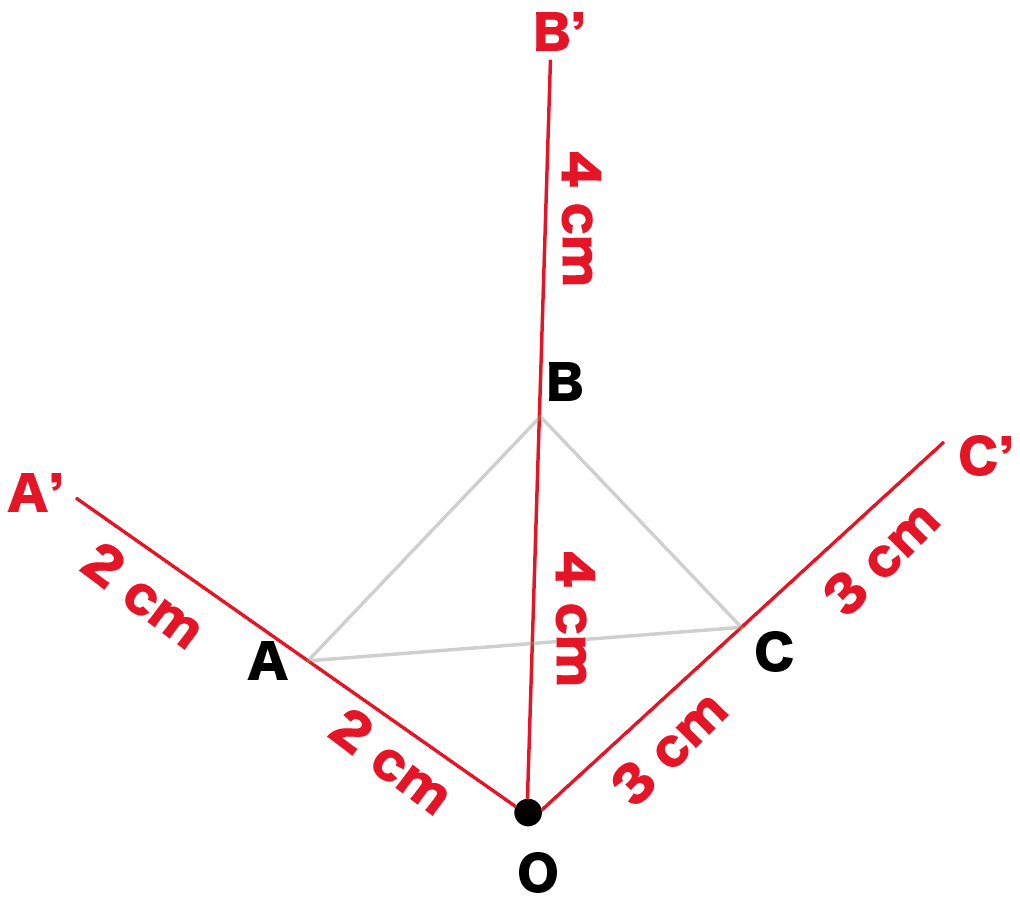
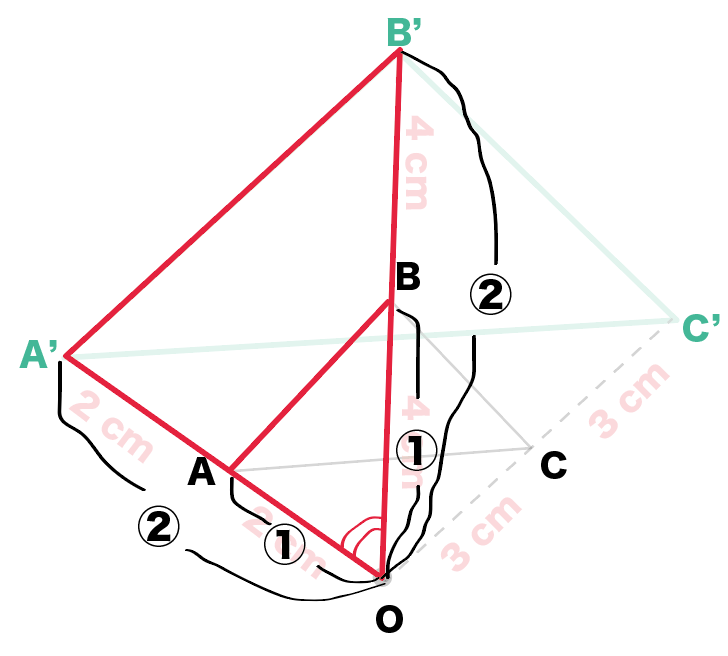
考相似な図形の性 質を見いだすことがで きる。 3 ①相似な 図形 図形の相似の意味や相似 な図形の性質について理解 する。 相似の中心と相似の 位置の意味について理 解する。 相似な位置にある図 形をかく。 相似比の意味につい て理解する。 前回の記事の最後に引き続いて, 相似変換 (中心相似) の応用を少しやってみる定円 内に定点 をとり, を通る弦 を引いて とせよ, という作図問題を考えてみる作図の解析をするために, 条件をみたす弦 が引けたと考えると, を相似の中心として, , であるから, は円 の周上の点でもある3 相似の位置にある図形を考え、いろ ・北海道の作図がどうしてかけたのかを考察するこ 1点を中心として相似な表現・処理 いろな方法でかく。 相似な図形を作図する とにより相似の位置にある図形のかき方を考え 図形をかいている。



Science 凸レンズで成り立つ公式 レンズの公式 写像公式 働きアリ The 2nd



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su



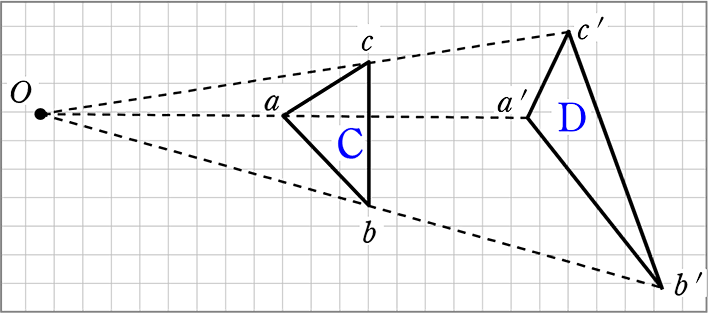
平面の変換




相似 作図 この問題の解説の 赤丸ぶぶんがよく分からないです Clear



2




号 図形表示プログラム サーバ 図形表示装置及び図形表示方法 Astamuse




レンズの公式 証明 導出 使い方 理系ラボ



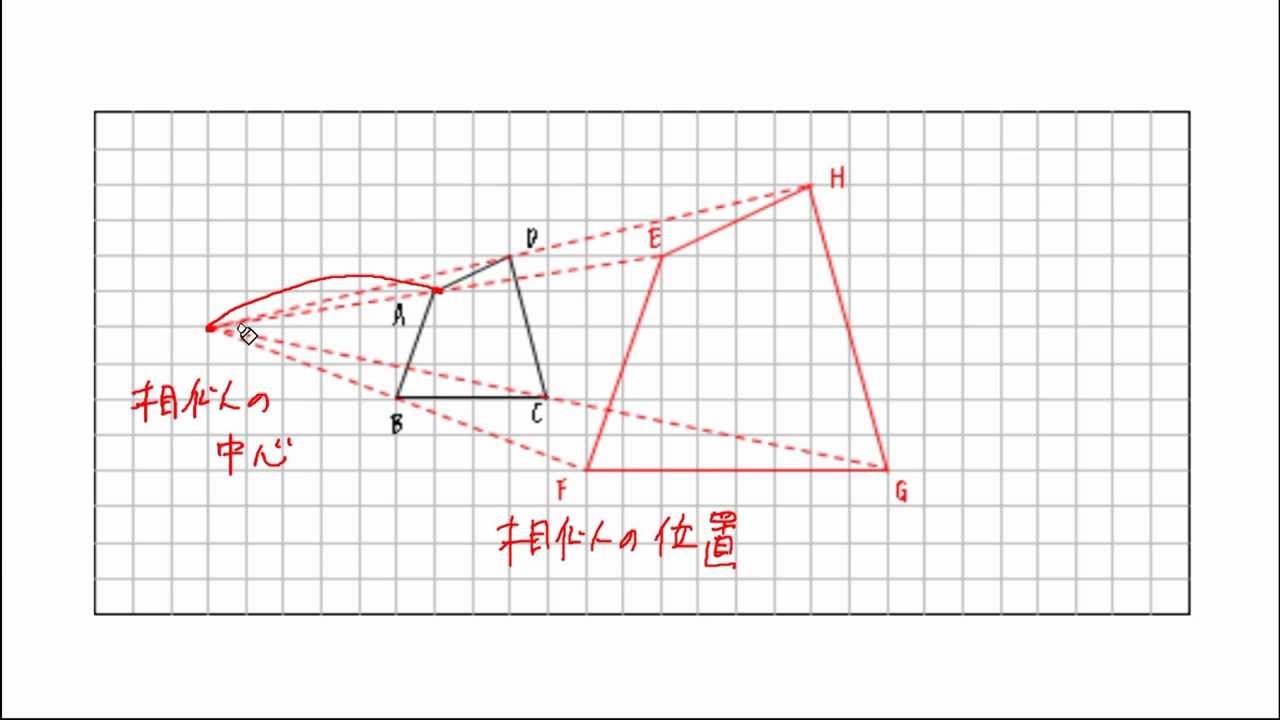
簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su



学習指導要領ナビ Jp 中学校 数学 第3学年の内容 b図形 図形の相似



結城浩 على تويتر 村上春樹の小説に 百科事典棒 という話が出てくるのを思い出しました 百科事典にある文字をすべてエンコードして 0 みたいな長い桁の数にして 爪楊枝のその位置に正確に刻み目をつけると 一つの刻み目が百科事典



Studydoctor相似の位置と中心 中3数学 Studydoctor




簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



中学数学 図形の相似



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋



前ちゃんの中学校数学の部屋 パワーポイント補助教材3年




高校物理 三角形の相似を駆使せよ 写像公式 波動 お茶処やまと屋



2



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 047 Pdf
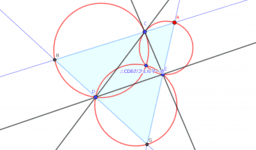



三角形に内接する三角形と外接する三角形の作図 Geogebra



中学3年 数学 相似の中心と作図 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



中学数学 図形の相似



相似の中心と作図 Youtube



Core Ac Uk Download Pdf Pdf



数学 時短演習cote



相似な図形 証明に慣れよう 苦手な数学を簡単に



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



相似の中心と作図 Youtube




相似な図形や中心の作図 中3数学 Youtube



Www Edu Yamanashi Ac Jp Modules Xelfinder Index Php View 1637 013 E9 95 E9 87 8e Pdf



レンズの公式 高校物理をあきらめる前に 高校物理をあきらめる前に



Http Www2 Gsn Ed Jp Houkoku 03c 03c07 03c08s Pdf



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




凸レンズの焦点距離 作図 虚像をイラストで即理解 高校生向け受験応援メディア 受験のミカタ




見てふれて 納得 中学校数学 おもしろ教材 授業アイデア 中学校数学サポートbooks 渋谷 久 本 通販 Amazon



1



2



Http Www Fdtext Com Dat Suub3 5zukei 1souji Pdf




鏡の演習問題 凹面鏡の式 焦点はどこ Physicmath フィジクマス




レンズの公式 高校物理をあきらめる前に 高校物理をあきらめる前に



相似な図形



Happylilac Net Pdf Jhs Math3 05 01ans Pdf



中学数学 図形の相似



Http Www1 Center Spec Ed Jp Action Common Download Main Upload Id




図形の合同 Wikipedia
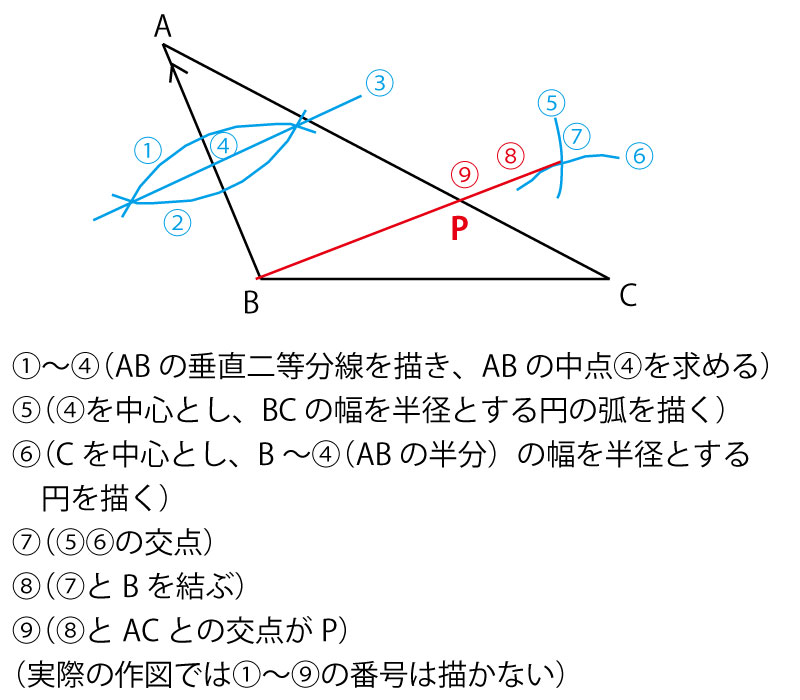



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
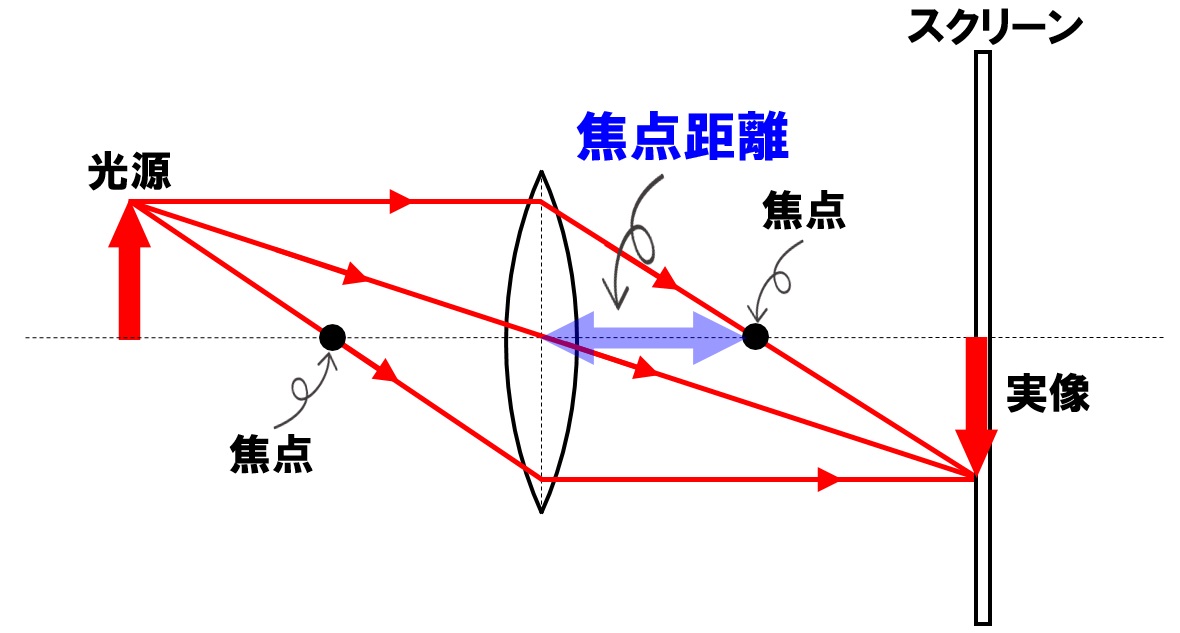



中1理科 焦点距離の求め方 作図や公式での求め方まで Pikuu



Studydoctor三角形の相似条件 中3数学 Studydoctor



相似な図形 基本事項を押さえる 苦手な数学を簡単に



三角形のオイラー線 9点円及びその周辺の話題
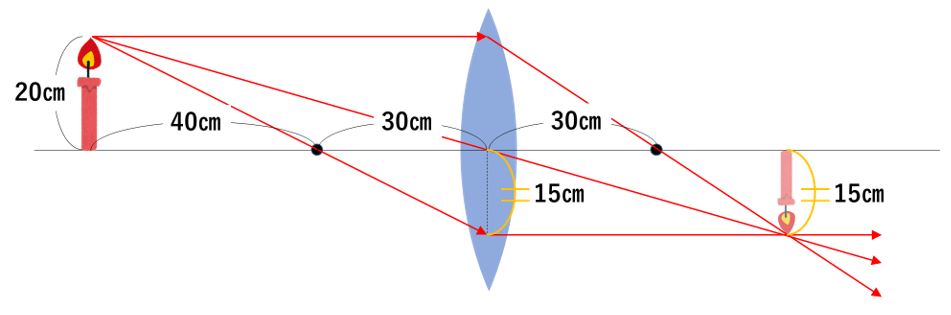



凸レンズの問題は作図を使って解こう 中学受験プロ講師ブログ



中学校数学 3年生 図形 相似な図形 Wikibooks




空間図形 線分を延長して相似な錐体を作って体積を求める問題 みみずく戦略室



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor



中1理科 焦点距離の求め方 作図や公式での求め方まで Pikuu




相似な図形 Ict教材eboard イーボード



数学の相似の図形の問題です分かる方 この問題の答えを教えてくださいこの Yahoo 知恵袋



Ousar Lib Okayama U Ac Jp Files Public 5 Papyrus 010 025 034 Pdf



Http Www Criced Tsukuba Ac Jp Renkei Msa Lessonplan Ooneda 2nd Medio Ooneda07 Jap Pdf



相似な図形



中学数学 図形の相似



Naoco Inc Ti Nspire Cx Cas 数式処理 グラフ 電卓 幾何 統計ソフト




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学



相似の記号と対応 On Vimeo



相似の例題解説 01 相似な図形 操作 目次の項目 をクリックすると 解答画面に行きます Rei1 Jpg 解答画面 拡大縮小の図形シミュレーター Rei011 Jpg 02 相似な図形のかき方 Rei2 Jpg 03 相似な図形のかき方 Rei3 Jpg 04 相似な図形の




相似を利用した作図問題 東久留米 学習塾 塾長ブログ
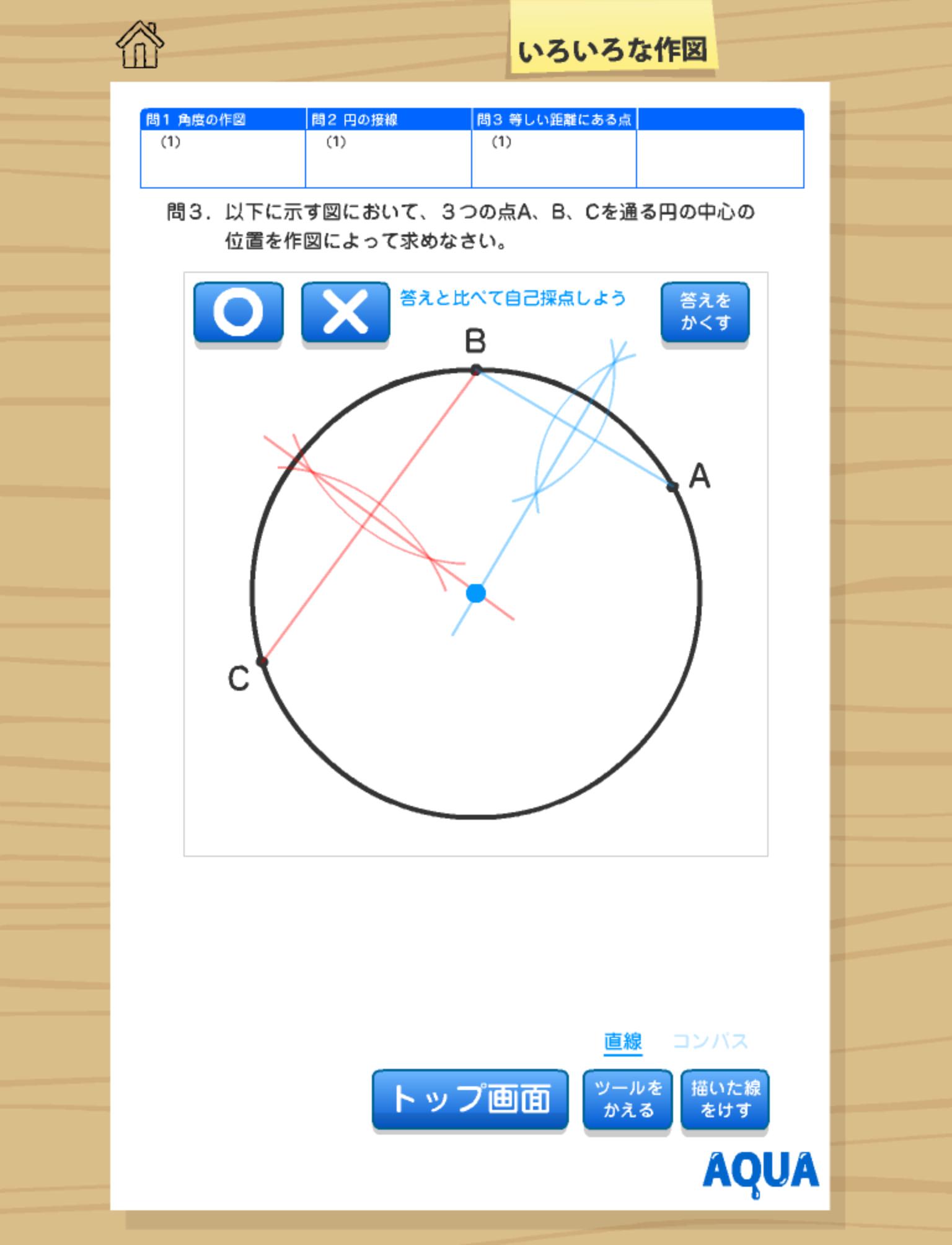



いろいろな作図 さわってうごく数学 Aquaアクア For Android Apk Download



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



Http Www Onomichi Ed Jp Mitsugi J Kyouiku Kennkyu R2 sidouan 4 80 80suugaku 1nen kaneko Pdf



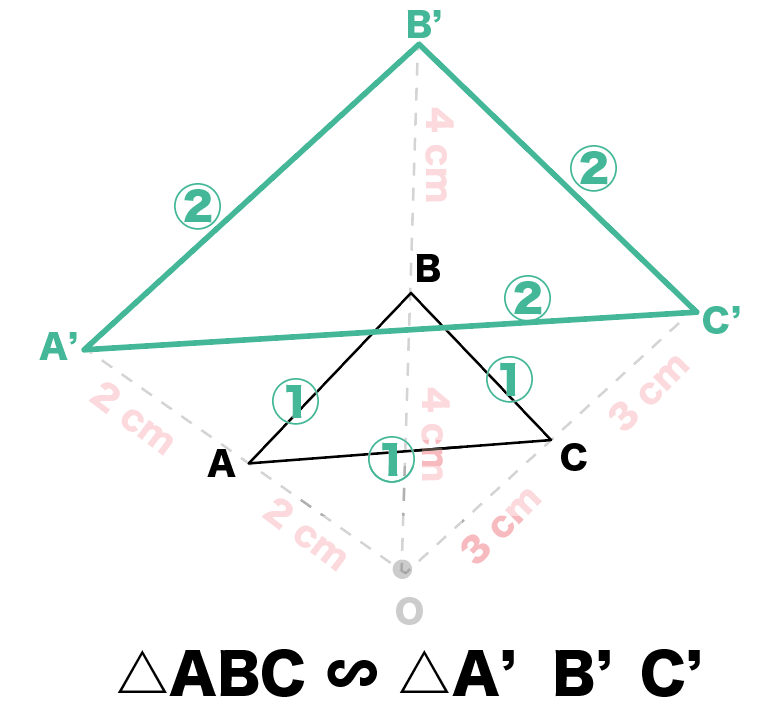
5章1節03 相似の位置と相似の中心 中村 翔
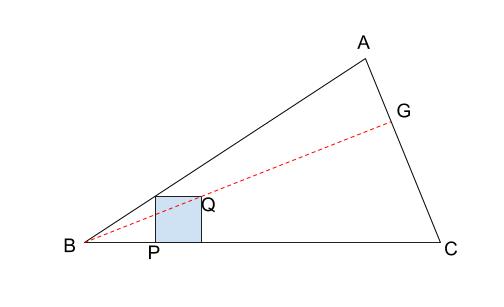



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su



1




中3数学 拡大図 縮図の作図 映像授業のtry It トライイット



単一ファイル一覧 Test Gc 4kaku Chuten Htm Gc 作図 Htm Gc 作図 Htm Gc 1 Htm Gc 4kaku Chuten 10 Htm Gc 4kaku Chuten 02 Htm Gc 4kaku Chuten 02 Htm Gc 5年合同 Htm



Http Www1 Iwate Ed Jp Db Db2 Sid Data Jh Sugaku H30 Jhsu115 Pdf




理科で登場する算数 図形編その1 相似 リカの中学受験理科ブログ




Acを1 2に分ける点pの作図 いつもお世話になります 16年 今年 の 数学 教えて Goo




図形の性質 作図 新課程数学a



2




相似 作図 この問題の解説の 赤丸ぶぶんがよく分からないです Clear




中3数学 拡大図 縮図の作図 練習編 映像授業のtry It トライイット




中3 相似の中心を利用した作図 勉強 Youtube スタディチューブ



Www Seg Co Jp Wp Content Uploads Sugaku No Sekai Question 1810 Pdf
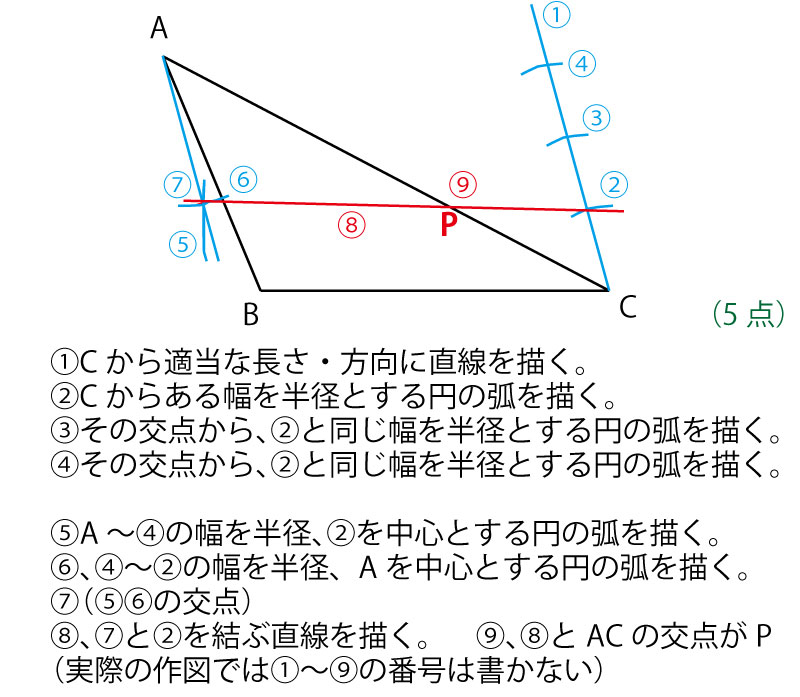



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
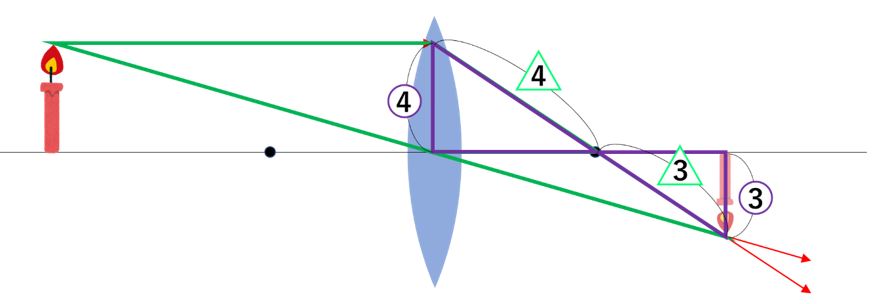



凸レンズの問題は作図を使って解こう 中学受験プロ講師ブログ
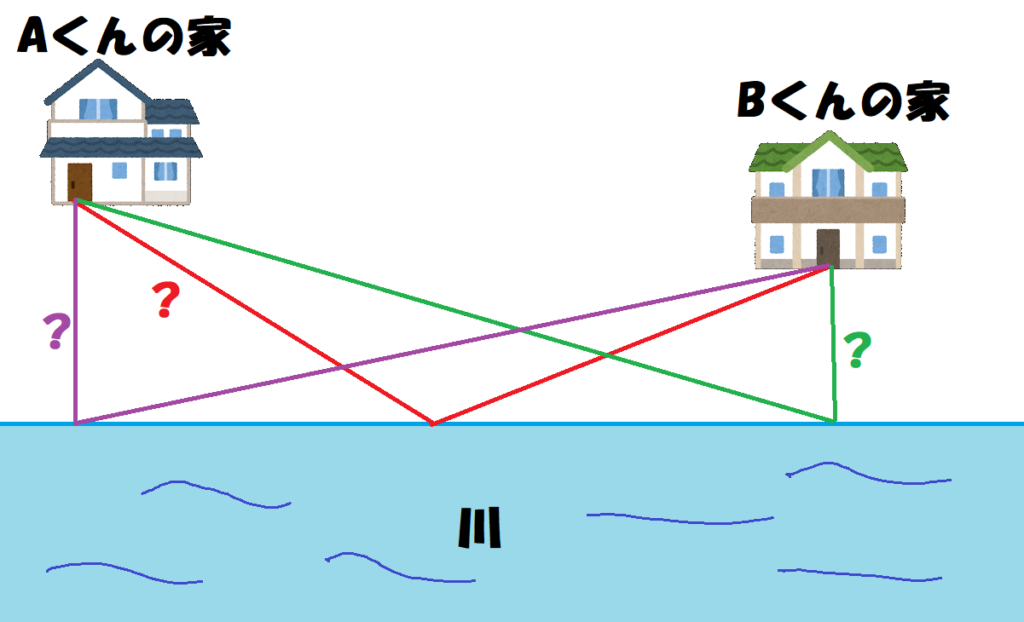



折れ線の最短距離 Fukusukeの数学めも



1




Euclidea 3 6 台形の底辺の中点の作図 解説 みのまわりのものたち



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



Www Pref Oita Jp Uploaded Attachment Pdf



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



相似の中心 中学から数学だいすき



No 動画コンテンツ タイトル 内容 形式 分 秒 01 滋賀の算額 神社に奉納された算額 数学の絵馬 にある問題を紹介 円周角の定理 相似 の考え方を使う 問題と図 Rm 4 1mb Wmv 4 4mb 2 01 02 滋賀の算額 ヒント 三平方の定理



0 件のコメント:
コメントを投稿