高校講座home >> 数学Ⅰ >> 第8回 数と式 無理数の近似値; Golangで、定積分の値の近似値を台形公式により求めて返す関数を作成しました。 プログラム中の integrate という関数が定積分の値を求める関数です。引数として、定積分する関数と、定積分の区間を渡します。引数とし 定積分の値の近似値を台形公式により求めて返す関数 の続きを・近似曲線を表示させる方法の式を出す方法 ・近似曲線の数式から値を求める方法 というテーマで解説していきます。 近似曲線を表示させる方法の式を出す方法 ある同じ種類の電池において、質量と値段には以下のような関係があるとします。

中1数学 近似値 練習編 映像授業のtry It トライイット
近似値 公式
近似値 公式-これは関数 = をテイラー展開したものである。 = (), =という常微分方程式の初期値問題の解 y(x) によって exp x = y(x) が定義2つの公式について、分割数n = 2~100 に対する 積分の近似値と 理論値の誤差の絶対値 (理論値) I を出力する。 ただし、シンプソンの公式の分割数は内部で(台形公式の)2倍になっているので、 分割数を偶数で増加させ、(台形公式の)半分にして比較する




ルートの近似値を計算する素朴な方法とコツ 高校数学の美しい物語
関数の近似とTaylor 展開 微分係数と接線の方程式 実数x の関数f(x) のx0 における微分係数f′(x 0) の定義は次の様に書き換えることが出来る。 lim x→x0 f(x)−f(x0) x−x0 −f′(x 0) = 0 つまり とおくと このことは を の近くで一次関数 で近似すると、 が に近付くとき「余り」 は のF(x) quadratic linear 図3 Simpson公式による数値積分。太線の"quadratic"が二次関数による被積分関数の近似曲線であ り、"linear"と書いてある台形則による近似より被積分関数の良い近似になっている。 となる。この式をSimpson シンプソン 公式と言う。2 区間a, bにわたる積分をするときは、二区このことから一般に N 等分した場合の近似値 s N と真の値 s との差は s N s < (f max f min) h f max ,f min は,(a,b) での最大値と最小値 であると考えてよい。 台形公式の場合,左端の区間 (a,ah) を考えてみよう。Taylor展開を用いれば,真の積分値は
0 < < ˇ 2) の扇形OAP を考え, P からx 軸に下ろした垂線の足をH,A にお ける接線と半直線OP の交点をT とすると, 高次の補正公式 ニュートン法でやっても良いのだが、特に逆数近似の補正はテイラー展開でやるほうがきれいなので、そっちでやる。 ある数 a に関して、逆数近似 a ~ 1 が得られたとしよう。 これを1次の近似と呼ぶ。 本来ならばある数とその逆数をこの公式とさきほどの常用対数の近似値から,自然対数の近似値を求めることができます! 例 log e 2 ≒ 23 ⋅ ≒ 07 \log_{e} 2\fallingdotseq 23\cdot \fallingdotseq 07 lo g
数学Ⅲ・C 公式集 <関数と極限> ① 分数関数 ax b cx b y = のとき割り算の商と余りを利用して x q r y p= と変形できる。 このときグラフは、漸近線が、 x=q,y=pの直角双曲線になる。 ② 無理関数 実は, 近似公式というのは ある量 x の何乗が 1 に対して無視できる状況なのか によって使う式が変わってくるのであるの尺度で102程 度精確であり,numpac(二 宮市三(19))の 単精度用の関数と同等の公式で あるま た,こ の近似式を使用する際,数 値計算上注意すべき事柄について述べる 2有 理関数近似式の誘導 q(u)の 近似式を求めるのに用いられる展開式のうち次式を用いる




近似値と誤差とは 中学1年数学 Youtube



Studydoctor近似値と誤差とは 中学1年数学 Studydoctor
よく使う一次近似の公式(不等式)一覧 高校物理で登場する近似式の多くが一次近似の形です。 一方,高校数学では「近似」は直接は問題にしにくいので不等式の形で活躍することが多いです。 近似式,関連する不等式,不等式が成立する範囲 の3点台形公式の数値実験 5 前と同じf(x)= 1 1x で実験してみる(cf daikeif). h =1/N 近似値動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → https//19chtv/ Twitter→ https//twittercom/haichi



数 近似値 近似式 数学のコツ




もう円周率で悩まない Pの求め方10選 プロクラシスト
高校数学Ⅲ階乗n!の近似式(スターリングの公式) 受験の月 階乗の近似式(スターリングの公式:n!≒ (n/e) n )ネイピア数を定義するために用いられる指数関数や対数関数の性質・公式を挙げる。これらの式と e = exp 1 などを組み合わせることによって、ネイピア数が定義できる。 = =! 15の続き (近似値計算) 資料解釈 さて、問題です。 100円のパンが、2回続けて、10%の値上げをしました。 いくらになったでしょうか?



60の近似値の求め方を教えてください 電卓を使う ではダメでしょうね Yahoo 知恵袋




数学 B 対数の近似値 関西大 立命館大 成蹊大 広島大 大学入試数学の考え方と解法
・tan^(1)の微分は 633 から・tan^(1)の級数展開は 857 から・電卓による値の計算は 10 からマチンの公式とπの近似値(前)はht長方形則ともいう。 定積分 を有限個の 長方形 で置き換えて近似的に求めるときに用いられる公式で,次のように表わされる。 ただし h = (b - a)/ n である。次に、上の K 、r、T、S、及び σ が与えられた時、積分値を M,M の範囲で n分割の台形公式によって求めるオブジェクトを構築する。そして、K=10、r=001、T=05、S=10、及び σ =01 の時、1,1 なる範囲で 2 8 個分割の台形公式による近似積分値を求めてみよう。



近似式の公式は どう証明すればよいのでしょうか 微分の公式でf A Yahoo 知恵袋




高校数学 近似値 平方根 円周率 常用対数 自然対数の底 のゴロ合わせ 受験の月
真 の 値 に 近 い値をいい、測定や近似計算によって得られる。 たとえば15℃の空気中の音の速さの近似値は毎秒340メートル、分数1/3の近似値は033、 円周率 の近似値は314などである。と計算していって, だんだん正確にして いける 誤差の評価値jS2n ¡Snj が指定の値より小さくなったらそこで やめる 樋口さぶろお(数理情報学科) 台形公式で数値積分 数値計算法L08() 14 / 16数学Ⅰ eテレ 毎週 月曜日 午後2:10~2:30 ※この番組は、21年度の新作です。



服部嗣雄 難問題の系統とその解き方 新課程 物理 の活用法と歴史




近似値
7月22日は円周率近似値の日とされている( 22 / 7 は円周率の近似値)。 12年 8月14日、米国勢調査局が、米国の人口が円周率と同じ並びの3億1415万9265人に達したと発表した。アメリカには円周率の曲を作る人もいる 。背景 22 / 7 は、 π の正則な連分数展開から得られる近似値の一つであり、又、表現が簡潔であることから π の近似値として広く用いられている。 22 / 7 が π よりも大きいことは、これらの値の十進法での小数展開 = ¯, = より分かる。 この近似値は古代より知られており、アルキメデスは紀元前π の近似値 このページでは過去発表された円周率の近似値を表す数式を紹介する。 元の表記方法(の日本語訳)をそのままを使うと(特に古い文献で) 円周率を求めた記述ではないというような解釈ができるが ここでは π = π = の形に解釈したものを
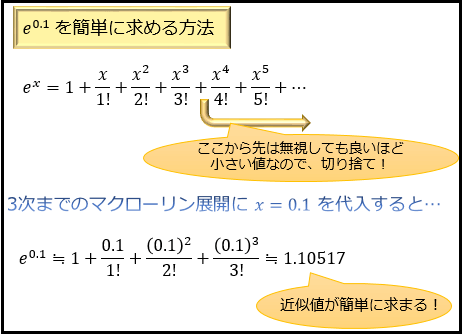



テイラー展開 マクローリン展開はどう使うのか 関数をシンプルに考える近似のテクニック アタリマエ




中1数学 近似値 練習編 映像授業のtry It トライイット
これを用いてマチンの公式でπの近似値計算を行ってみると,級 数計算でn=713 程度までの和を計算すれば,1000 桁まで一致する. このnの値を小さくできて,係数がクレージーでない公式を作る ことが,C君の当面の目標である.ちなみに改良版*ではn=435 程= である。 O(log n) における次の項は (1/2)log 2 π n である。 故に、次によい近似の 漸近公式 (英語版) は !台形公式(台形則) 最も単純なものは2点間を直線で結ぶ,即ち1次多項式で近似し,その補間多 項式を積分して近似値を求める,いわゆる台形公式(trapezoidal rule)である。図 形的にはちょうど分割した関数とx座標で囲まれる台形の面積を求め,それを全




ルートの近似値を計算する素朴な方法とコツ 高校数学の美しい物語




立川高校クイズ研究部公式アカウント Di Twitter 昨日のペーパークイズを公開します 最高点は37点 シードボーダーは25点 近似値ピタリ 抽選 でした Qmt3rd
常用対数の近似値の算出 対数は「底 x の値を何乗したら z になるか? 」の指数を求めるもの、指定するものと捉える。 z = x y での y を知りたい場合に y = log x z と書く。 対数関連の公式 常用対数は、対数の底が10のもの。 (※自然対数は対数の底Rubyによるπの近似値計算 情報班:森川大翔 市村奉紀 1.研究内容 rubyというプログラミング言語を用いて円周率を近似した。今回は、ライプニッツ の公式とガウス=ルジャンドルのアルゴリズムを用いて、二つの方法でπの近似値を 求めた。Taylor の定理の応用:誤差評価付きの近似値計算1 ここでは正確な値がわからない無理数について,その近似値をテイラー の定理(マクローリンの定理)を用いて計算してみる. 例題 ネイピア数e の近似値を求めよ. 解答(Part 1)




徹底図解 テイラー展開の公式 意味 具体例を超分かりやすく解説するよ てつたま
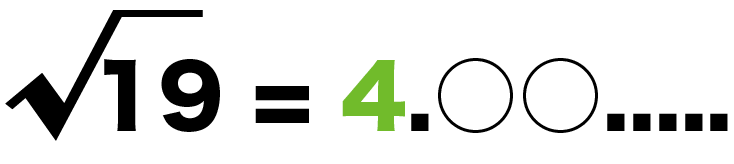



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく
1706年、イギリスのジョン・マチンによって示された公式です。 非常に収束速度が速い級数が使われていて、円周率の 1 4 1 4 の値を求めることができるため、ジョン・マチンは円周率の近似値を100ケタまで計算しました。H は十分小さいが有限(無限小ではない)の正の値をもつとする。h2 ≪ h だから,h の2 乗以上の項を無視し て式変形すると,次の前進差分近似公式が得られる。 f′(x) ≃ f(x h) − f(x) h (73) 712 後退差分近似 関数のTaylor 展開は,次のようなものも考えられる。 マイナビニュース公式SNS 連載 第40回 Excelデータ分析の基本ワザ 近似曲線を利用するときの注意点 0901 近似曲線と平均値について




人類の至宝 オイラーの公式は 宇宙の真理に近づくための近似値計算のために考案された 発想力教育研究所 素数誕生のメカニズム
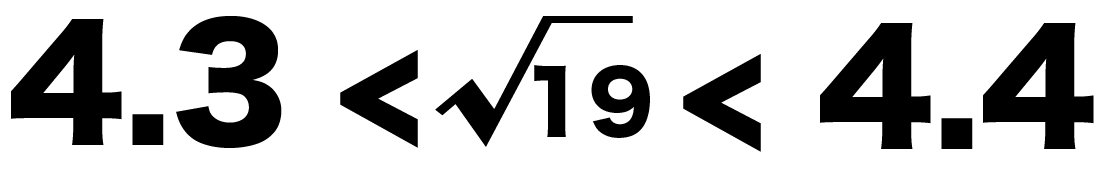



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく
である 。 。(ここで記号 は両辺の比が(n → ∞ のとき台形公式とシンプソン公式の誤差 台形公式の誤差 台形公式による積分の近似値 I は,真の積分値に対し てどのくらい良い近似値になっているだろうか。前節で導いたラグランジュ 補間の誤差の評価式を用いると,この疑問に答えることができる。 いま, f x Cχ2 =z 12 z 22 ···z n2 ※ このように「 カイ2乗分布(χ 2 分布) 」は,もともと数学的に定義された連続関数に付けられた名前である. これに対して「カイ2乗検定」に登場する「 カイ2乗 」はm×n分割表などにおいて各セル(窓枠)に入ったデータの観測




微分法とその応用 の記事一覧 受験辞典




Log10 2からlog10 5を求める方法は Log10 2 A Log10 3 B とする時のlog10 15の計算方法は Log2 10 の 近似値の覚え方 ウルトラフリーダム
1 第1章 三角関数の極限と近似 三角関数の極限 ⃝1 lim →0 sin = 1 ···(基本公式) ⃝2 lim →0 1−cos 2 = 1 2 ···(準公式) x y O A(1;0) P T H 証明単位円上に,中心角が (単位はラジアンで;



平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典




高校数学 対数log Abの近似値求め方 評価の方法 受験の月




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




ルートの近似値を計算する素朴な方法とコツ 高校数学の美しい物語




Cプログラミング演習 ニュートン法による方程式の求解 Ppt Download
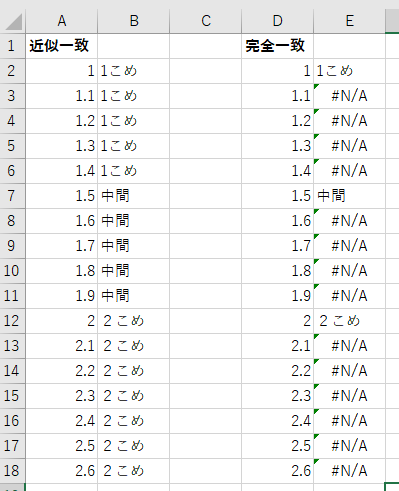



Vlookup関数の 近似値 条件true の実際の動作を 徹底検証する 志木駅前のパソコン教室 キュリオステーション志木店のブログ




数学 近似式まとめ 各種公式 求め方 理系ラボ



ライプニッツの公式で円周率を求めるプログラムなのですが 例えばnに100を Yahoo 知恵袋




高校数学 近似値の計算 問題編 映像授業のtry It トライイット



3




中1 数学 中1 近似値 Youtube



ガイダンス




近似値から真の値の範囲を求める 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信




平方根の活用 式の値と近似値の求め方 教遊者




中3数学 平方根の近似値 映像授業のtry It トライイット




平方根 近似値を求める 苦手な数学を簡単に




近似計算 高校物理をあきらめる前に 高校物理をあきらめる前に




近似式とは 練習問題で微分の応用を理解しよう 高校生向け受験応援メディア 受験のミカタ




スプリックス 近似値と誤差 有効数字 2 Youtube




数 132 近似式 Youtube




高校数学 数 動画 近似式の問題 19ch




高校数学 関数f X の1次近似式 映像授業のtry It トライイット




円 周 率 物 語 Ppt Download




中1 数学 資料の整理7 近似値とは 13分 Youtube




高校生も納得 テイラー展開 マクローリン展開の証明と使い方 高校生向け受験応援メディア 受験のミカタ




ラマヌジャンの円周率公式 Tsujimotterのノートブック




Pの近似値について 身勝手な主張



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




6 の正しい近似値を教えてください 左がネット 右が教科書 です Clear




中1数学 近似値 練習編 映像授業のtry It トライイット




近似値と有効値 数学の要点まとめ 練習問題一覧




2の近似値の求め方の説明の意味が分かりません Clear




マチンの公式とpの近似値 後 Youtube




中1数学 近似値 練習編 映像授業のtry It トライイット




円 周 率 物 語 Ppt Download




練習7が分からないです Clear



平方根の活用 式の値と近似値の求め方 教遊者




数学 近似式まとめ 各種公式 求め方 理系ラボ




数学 近似式まとめ 各種公式 求め方 理系ラボ



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




微分積分学 基礎数学 7回目




近似計算 高校物理をあきらめる前に 高校物理をあきらめる前に




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく



近似値 近似式とは 公式や求め方 テイラー展開 マクローリン展開も 受験辞典
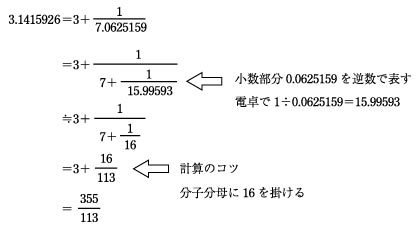



数学切り抜き帳




円 周 率 物 語 Ppt Download



平均値の求め方 近似値 真の値 誤差の求め方 中学1年数学 資料の分析と活用




スターリングの公式でn の近似値を求める いぬおさんのおもしろ数学実験室




テイラー展開とは イメージ 式の意味 使い方を具体例で解説
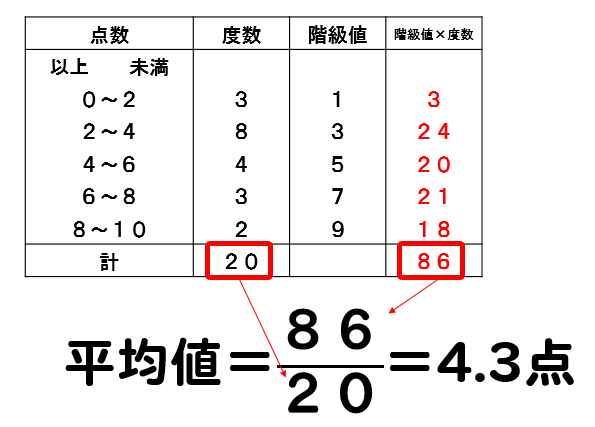



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




平方根のおよその値の求め方とその利用 わかるようになる高校数学



Q Tbn And9gcrxte7kpw Prbp1ha Goiskrvwgvrgwheflvtt1dxkyal9yqqhz Usqp Cau




中3 ルートの近似値の求め方をイチから解説 Youtube



Studydoctor ルートの近似値の求め方 中3数学 Studydoctor



電位増分dvを求める全微分公式が近似値となることの説明 Jo3krpの独り言




一次近似の意味とよく使う近似公式一覧 高校数学の美しい物語




ルート3の近似値の求め方4パターン 数学の星




一次近似の意味とよく使う近似公式一覧 高校数学の美しい物語




近似値と有効数字の求め方とは どちらも情報の 度が大事 遊ぶ数学



1




基礎数学 10回目




平方根の活用 式の値と近似値の求め方 教遊者



Http Trail Tsuru Ac Jp Dspace Bitstream Trair 870 1 Y 0039 Pdf




高校数学 近似値の計算 問題編 映像授業のtry It トライイット




漏れたダミーは 公式のiphone13モデルに最も近い近似値である可能性があります Ja Atsit



1




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




数学 近似式まとめ 各種公式 求め方 理系ラボ




マクローリン展開 三角関数のマクローリン展開の計算 空間情報クラブ 株式会社インフォマティクス




中1数学 近似値と誤差の求め方の定期テスト予想問題 Pikuu




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




近似値を使わずに対数の値を比較する いぬおさんのおもしろ数学実験室




数学 近似式まとめ 各種公式 求め方 理系ラボ
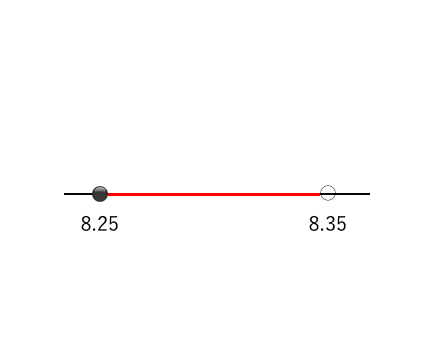



近似値の問題 苦手な数学を簡単に




画像 ルート 展開 近似 ハイキュー ネタバレ




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




近似値と有効値 数学の要点まとめ 練習問題一覧




3がいきなり1 73となっていますが ひょっとして物理は の近似値を暗記してあるこ Clear




近似値を概数を使って求める場合です 下の問題で何でsin61 じゃなく Okwave




データの分析 無理数の近似値の求め方 数学 定期テスト対策サイト
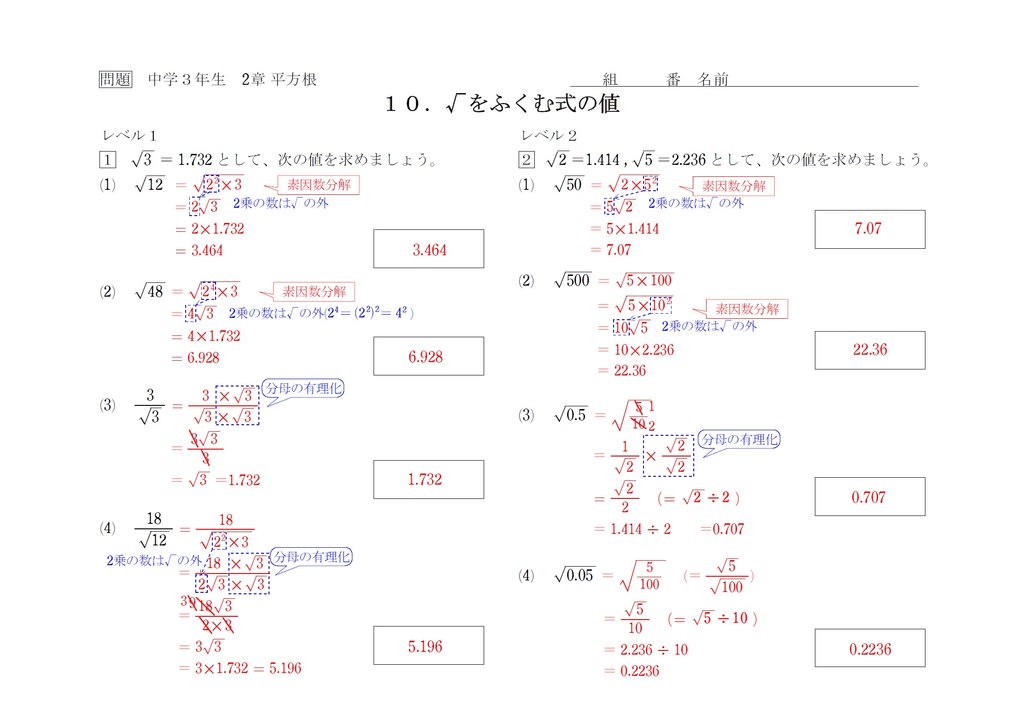



中3 平方根10 近似値 中学数学の勉強に



近似値ってどうやって求めるんでしたっけ そもそも近似値と Yahoo 知恵袋



68 08の小数点以下の近似値の求め方を教えてください Yahoo 知恵袋



0 件のコメント:
コメントを投稿